General Principle of Convergence
Suppose that $(a_n)$ is a sequence of real numbers. If we suspect that its limit is $L$, we can study the behaviour of $\vert a_n - L \vert$ as $n \to \infty$. However, we might not know what $L$ should be and still want to study the convergence of the sequence. Therefore, we need a more general way to define convergence.
Definition. [Cauchy Sequence] $(a_n)$ is a Cauchy sequence if
\[(\forall \varepsilon > 0)(\exists N \in \mathbb{N})(\forall m, n \ge N)\; |a_m - a_n| < \varepsilon\]
So instead of comparing the terms with a certain value, we check if the terms become close as $m$ and $n$ become large.
Lemma. A Cauchy sequence is bounded.
Proof.
There exists a $N$ such that for all $m, n \ge N$, $\vert a_m - a_n \vert < 1$. Let
\[M = \max(|a_0|, |a_1|, ..., |a_N|, |a_N + 1|)\]For all $n > N$,
\[|a_n| \le |a_n - a_N| + |a_N| < |a_N| + 1\]so $\vert a_n \vert \le M$ for all $n$ and $(a_n)$ is bounded.
Theorem. [General Principle of Convergence] A sequence $(a_n)$ of real numbers is convergent iff it is a Cauchy sequence.
Proof.
($\Rightarrow$) If $(a_n)$ is convergent to $L$, there exists an $N$ such that $\vert a_n - L \vert < \varepsilon / 2$. Therefore, for $m, n \ge N$,
\[|a_m - a_n| \le |a_m - L| + |a_n - L| < \varepsilon / 2 + \varepsilon / 2 = \varepsilon\]and $(a_n)$ is Cauchy sequence.
($\Leftarrow$) If $(a_n)$ is a Cauchy sequence, it is bounded. By the Bolzano-Weierstrass theorem, there exists a subsequence $(a_{n_k})$ convergent to some value $L$. For $\varepsilon > 0$, there exists a $K$ such that $\vert a_{n_K} - L \vert < \varepsilon / 2$ for $k > K$ and also a $N$ such that $\vert a_m - a_n \vert < \varepsilon / 2$ for $m, n \ge N$. Therefore, for some $k \ge K$ such that $n_k > N$ and $n > N$, we have
\[|a_n - L| \le |a_n - a_{n_k}| + |a_{n_k} - L| < \varepsilon / 2 + \varepsilon / 2 = \varepsilon\]
Limit Supremum and Infimum
There is something more we can say about the limit $L$ which we might not be able to find. Suppose that $(a_n)$ is a bounded sequence. $(M_n = \sup \Set{a_k : k \ge n})$ is decreasing (as we take suprema over smaller and smaller set) and bounded below therefore it converges. Similarily, $(m_n = \inf \Set{a_k : k \ge n})$ is increasing and bounded above therefore it converges.
Definition. The limit supremum of a sequence $(a_n)$ is the limit of the subsequent suprema, i.e.
\[\limsup_{n \to \infty} a_n = \lim_{n \to \infty} \left( \sup_{m \ge n} a_m \right)\]
Definition. The limit infimum of a sequence $(a_n)$ is the limit of the subsequent infima, i.e.
\[\liminf_{n \to \infty} a_n = \lim_{n \to \infty} \left( \inf_{m \ge n} a_m \right)\]
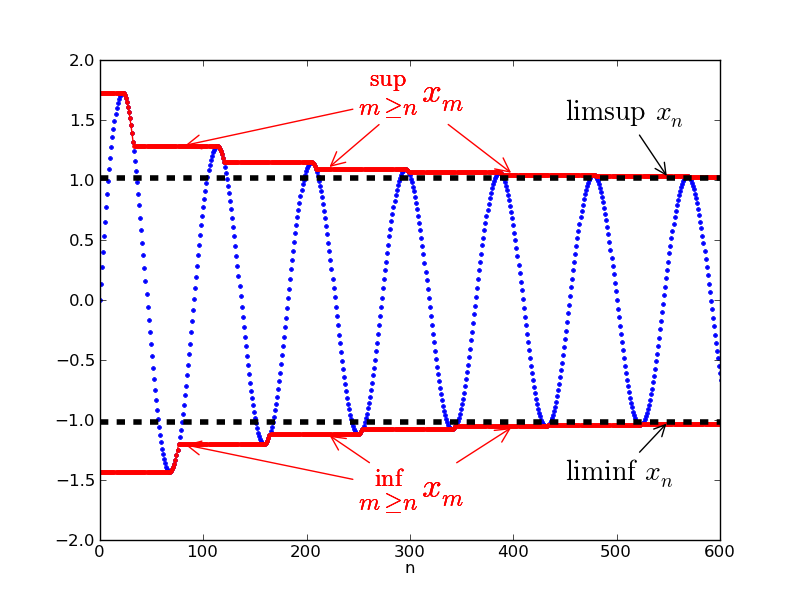
These limits are a little complicated, being defined in two stages, we first form a sequence of suprema/infima and then take the limit of it. Their fundamental properties can be useful in some cases.
Property. Suppose that $(a_n)$ is a bounded sequence, and $S = \limsup_{n \to \infty} a_n$. Then $S$ is the unique real number with the two following properties:
if $t > S$ then there exists $N$ such that $a_n < t$ for all $n > N$;
if $r < S$ and $n \in \mathbb{N}$ then there exists $m \ge n$ such that $a_m > r$.
It is equivalent to saying $a_n$ is eventually less than $t$ and frequently greater than $r$.
Property. As $\inf a_n \le \sup a_n$, we have
\[\liminf_{n \to \infty} a_n \le \limsup_{n \to \infty} a_n\]
Theorem. Suppose that $(a_n)$ is a bounded sequence. Then $a_n \to L$ iff $\limsup a_n = \liminf a_n = L$.
($\Rightarrow$) For $\varepsilon > 0$, there exists an $N$ such that $L - \varepsilon/2 < a_n < L + \varepsilon/2$ for all $n \ge N$. Therefore,
\[L - \varepsilon < \inf_{m \ge n} a_m \le \sup_{m \ge n} a_m < L + \varepsilon\]and $\limsup a_n = \liminf a_n = L$.
($\Leftarrow$) As $\limsup a_n = \liminf a_n = L$ and
\[\inf_{m \ge n} a_m \le a_n \le \sup_{m \ge n} a_m\]By Sandwich Principle, $a_n \to L$.
References
- D. J. H. Garling A Course in Mathematical Analysis Vol.1, 2013 - Chapter 3.5, 3.6