Integrability
The concept of a definite integral was developed to represent an area bounded by curved lines. This geometrical equivalence is helpful to visualize the meaning of the analytical expressions occur in the defintion and manipulation of integrals.
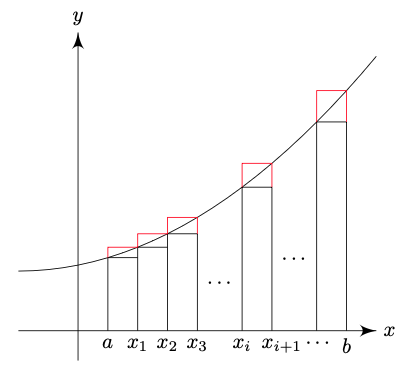
Definition. A dissection of an interval $[a, b]$ is a finite set of numbers $a, x_1, x_2, …, x_{n-1}, b$ such that
\[a < x_1 < x_2 < \cdots < x_{n-1} < b\]To complete the scheme, we write $a = x_0$ and $b = x_n$. Each $x_r$ is a point of division.
The dissection splits $[a, b]$ into $n$ subintervals, i.e. $I_1 = [x_0, x_1]$ and $I_r = (x_{r-1}, x_r]$.
The length of the $r$th subinterval is $\delta_r = x_r - x_{r-1}$, and the greatest length $\delta^\ast = \max \delta_r$ is called the norm/mesh size of the dissection.
Definition. The upper sum $S_D$ and lower sum $s_D$ are defined by
\[\begin{align*} S_D(f) &= \sum_{r = 1}^n \delta_r \sup_{x \in I_r} f(x) \\ s_D(f) &= \sum_{r = 1}^n \delta_r \inf_{x \in I_r} f(x) \end{align*}\]
The upper sum is the total area of the red rectangles and lower sum is that of black rectangles.
Definition. If every point of $D_1$ is a point of $D_2$, then $D_2$ is a refinement of $D_1$, i.e. $D_1 \le D_2$.
Proposition. If $D_2$ refines $D_1$, then
\[S_{D_2} \le S_{D_1} \quad \text{and} \quad s_{D_2} \ge s_{D_1}\]Proof.
Suppose $D_2$ refines $D_1$ by introducing a new point of division $x_r’$ into $I_r$ which divides the interval into $I_{r’}$ and $I_{r’'}$. Then we have $\sup_{x \in I_{r’}} f(x) \le \sup_{x \in I_r} f(x)$ and $\sup_{x \in I_{r’'}} f(x) \le \sup_{x \in I_r} f(x)$ and
\[\delta_{r'} \sup_{x \in I_{r'}} f(x) + \delta_{r''} \sup_{x \in I_{r''}} f(x) \le \delta_{r} \sup_{x \in I_{r}} f(x)\]Hence, $S_{D_2} \le S_{D_1}$. Similarily, $s_{D_2} \ge s_{D_1}$.
Definition. The least common refinement of $D_1$ and $D_2$ is the dissection made out of points of $D_1$ and $D_2$, denoted by $D = D_1 \vee D_2$.
Proposition. Let $D_1$ and $D_2$ be any two dissections of the same interval $[a, b]$. Then
\[S_{D_1} \ge s_{D_2}\]Proof.
Let $D_3$ be the least common refinement of $D_1$ and $D_2$. By the above,
\[S_{D_1} \ge S_{D_3} \ge s_{D_3} \ge s_{D_2}\]
We can now define integral using the above machinary.
Upper and Lower Riemann Integrals
Definition. The upper and lower Riemann integral are defined by
\[J = \overline{\int_a^b} f = \inf_{D} S_D(f) \quad \text{and} \quad j = \underline{\int_a^b} f = \sup_{D} s_D(f)\]
Proposition. $\overline{\int_a^b} f \ge \underline{\int_a^b} f$.
Proof.
For any two dissections $D_1$ and $D_2$, we have $S_{D_1} \ge s_{D_2}$. Hence,
\[\overline{\int_a^b} f = \inf_{D} S_D \ge \sup_{D} s_D = \underline{\int_a^b} f\]
In fact, we do not need to consider all the dissections to determine the upper and lower Riemann integrals.
Proposition. Suppose that $(D_n)$ is a sequence of dissections of $[a, b]$ and that $\delta^\ast(D_n) \to 0$ as $n \to \infty$. If $f$ is a bounded function on $[a, b]$ then $S_{D_n}(f) \to \overline{\int_a^b} f(x)dx$ as $n \to \infty$.
Proof.
Suppose that $\varepsilon > 0$. Since $J$ is the infimum, there exists a dissection $D$ of $[a, b]$ with $k+1$ points of dissection such that $J \le S_D < J + \varepsilon/2$.
Let $\delta = (\varepsilon/2)(k+1)(M - m + 1)$, there exists $N$ such that $\delta^\ast(D_n) < \delta$ for all $n \ge N$. For any $n > N$, let $D’ = D \vee D_n$, we have $S_{D’} \le S_D$. Consider the subintervals of $D_n$ and $D’$, namely $\Set{I_1, …, I_q}$ and $\Set{K_1, …, K_s}$. Since $D’$ refines $D_n$, for each subinterval $I_p$, either $I_p = K_r$ for some $r \in \Set{1, …, s}$, or it contains one or more elements of $D$ which makes $I_p$ a disjoint union of finitely many subintervals of $D’$, i.e. $I_p = \bigcap_{r \in S_p} K_r$. Since $m \le f(x) \le M$, we have
\[M \delta_{I_p} \ge M_{I_p}\delta_{I_p} \ge \sum_{r \in S_p} M_{K_r} \delta_{K_r} \ge m \sum_{r \in S_p} \delta_{K_r} = m \delta_{I_p}\]Let $P$ be the set of indices of the subintervals of the latter case, we have $\vert P \vert \le k + 1$. Thus,
\[\begin{align*} S_{D_n} - S_{D'} &= \sum_{p \in P} \left( M_{I_p} \delta_{I_p} - \sum_{r \in S_p} M_{K_r} \delta_{K_r} \right) \\ &\le \sum_{p \in P} \left( M \delta_{I_p} - m \delta_{I_p} \right) \\ &\le (M - m)(k+1)\delta^\ast(D_n) < \varepsilon / 2 \end{align*}\]Consequently, we have
\[J \le S_{D_n} < S_{D'} + \varepsilon/2 \le S_D + \varepsilon/2 < J + \varepsilon\]and so $S_{D_n} \to J$ as $n \to \infty$.
Riemann Integrals
Definition. A bounded function $f$ on $[a, b]$ is Riemann integrable if its upper and lower integrals are equal, i.e. $J = j$. The common value is then the Riemann integral
\[\int_a^b f(x)\,dx\]
Proposition. [Riemann’s/Cauchy’s Integrability Criterion] A bounded function $f$ is Riemann integrable iff given $\varepsilon > 0$ there exists a dissection $D$ such that
\[S_D - s_D < \varepsilon\]Proof.
($\Rightarrow$) If there exists $D$ such that $S_D - s_D < \varepsilon$ then obviously $\inf S_D - \sup S_D < \varepsilon$. By definition, it means $J - j < \varepsilon$. Since $\varepsilon$ is arbitrary, it is only possible when $J = j$ so $f$ is integrable.
($\Leftarrow$) Suppose that $f$ is integrable. Then there exists dissections $D_1$ and $D_2$ such that
\[S_{D_1} < J + {\varepsilon \over 2} \quad \text{and} \quad s_{D_2} > j - {\varepsilon \over 2}\]Let $D = D_1 \vee D_2$. Then $S_D - s_D \le S_{D_1} - s_{D_2} < J - j + \varepsilon = \varepsilon$.
We can also characterize Riemann integrability in terms of a sequence of dissections.
Proposition. Suppose that $(D_n)$ is a sequence of dissections of $[a, b]$ and that $\delta^\ast(D_n) \to 0$ as $n \to \infty$. A bounded function $f$ is Riemann integrable iff $S_{D_n} - s_{D_n} \to 0$ as $n \to \infty$. If so,
\[\int_a^b f(x) \,dx = \lim_{n \to \infty} S_{D_n} = \lim_{n \to \infty} s_{D_n}\]Proof.
Base on the fact that $S_{D_n} \to J$ and $s_{D_n} \to j$ as $n \to \infty$ and $J = j$.
Proposition. Suppose that $(D_n)$ is a sequence of dissections of $[a, b]$ and that $\delta^\ast(D_n) \to 0$ as $n \to \infty$. A bounded function $f$ is Riemann integrable iff for any $\xi_r \in I_r$ of dissection $D_n$ with subintervals $\Set{I_1, …, I_{k_n}}$,
\[\sum_{r = 1}^{k_n} f(\xi_r) \delta_{I_r} \to l\]as $n \to \infty$. If so, $l = J$.
Proof.
($\Leftarrow$) If $f$ is Riemann integrable, then
\[s_{D_n} \le \sum_{r = 1}^{k_n} f(\xi_r) \delta_{I_r} \le S_{D_n}\]Since both $S_{D_n} \to J$ and $s_{D_n} \to J$ as $n \to \infty$, by Squeeze theorem, the sum tends to the limit $J$.
($\Rightarrow$) Suppose that $\varepsilon > 0$. There exists $\delta$ such that for any dissection $D_n$ with $\delta^\ast(D_n) < \delta$,
\[J - {\varepsilon \over 4} < \sum_{r = 1}^{k_n} f(\xi_r) \delta_{I_r} < J + {\varepsilon \over 4}\]in which $\xi_r$ is arbitrary. Choosing $\xi_r$ such that $f(\xi_r) > M_{I_r} - \varepsilon / 4k_n$ and therefore
\[S_{D_n} = \sum_{r=1}^{k_n} M_{I_r} \delta_{I_r} < \sum_{i=1}^{k_n} f(\xi_r) \delta_{I_r} + {\varepsilon \over 4} < J + {\varepsilon \over 2}\]Similarily, choosing another $\xi_r$ such that $f(\xi_r) < m_{I_r} + \varepsilon / 4k_n$ and therefore
\[s_{D_n} = \sum_{r=1}^{k_n} m_{I_r} \delta_{I_r} > \sum_{i=1}^{k_n} f(\xi_r) \delta_{I_r} - {\varepsilon \over 4} > J - {\varepsilon \over 2}\]Hence, $S_{D_n} - s_{D_n} < \varepsilon$ and $f$ is integrable.
Note that a function has to be bounded in the interval so to be Riemann integrable, otherwise its upper/lower integrals can’t be undefined. However, there are definitely unbounded functions that are integrable which leads to more sophisticated definiton such as Lebesgue integral.
Improper Integral
Definition. Suppose that we have a function $f$ such that, for every $\varepsilon > 0$, $f$ is integrable on $[a + \varepsilon, b]$ and $\int_{a + \varepsilon}^b f(x) \,dx \to l$ as $\varepsilon \to 0$. Then we define the improper integral
\[\int_a^b f(x) \,dx = \lim_{\varepsilon \to 0} \int_{a + \varepsilon}^b f(x) \,dx = l\]We can do similarily for $[a, b - \varepsilon]$ or integral to infinity.
References
- J C Burkill A First Cource in Mathematical Analysis, 1978 - Chapter 7
- D. J. H. Garling A Course in Mathematical Analysis Vol.1, 2013 - Chapter 8.2, 8.3