Difference Equations
Difference equations can appear in numerical approximations and other problems that the independent variable only takes discrete values.
Definition. The order of a difference equation is the largest difference between any two of the indices of $x$.
First Order + Homogeneous + Linear
Proposition. For a first order linear difference equation
\[x_{n+1} = kx_n\]the solution is
\[x_n = k^n x_0\]
Second Order + Homogeneous + Linear
The way of solving linear difference equations is analogous to that of differential equations.
Proposition. Consider a difference equation of the form
\[ax_{n+2} + bx_{n+1} + cx_n = 0\]Let $x_n = k^n$ be the solution. Then
\[ak^{n+2} + bk^{n+1} + ck^n = 0\]and cancelling $k^n$ gives us the auxiliary equation
\[ak^2 + bk + c = 0\]
Proposition. If the auxiliary equation has two distinct real roots $k_1$ and $k_2$, then the general solution is
\[x_n = Ak_1^n + Bk_2^n\]
Proposition. If the auxiliary equation has one repeated root $k$, then the general solution is
\[x_n = Ak^n + Bnk^n\]
Proposition. If the auxiliary equation has two complex roots $k = a \pm bi = r e^{i\theta}$, then the general solution is
\[x_n = r^n(A\cos n\theta + B\sin n\theta)\]Proof.
The complex roots can be handled just like they are real, i.e.
\[\begin{align*} x_n &= C(re^{i\theta})^n + C^\ast(re^{-i\theta})^n \\ &= r^n[2\text{Re}(Ce^{in\theta})] \\ &= r^n[2\text{Re}((\alpha + \beta i)(\cos n\theta + i \sin n\theta))] \\ &= r^n[2(\alpha \cos n \theta - \beta \sin n \theta)] \\ &= r^n(A \cos n \theta + B \sin n \theta) \end{align*}\]
Second Order + Inhomogeneous + Linear
Proposition. Consider a difference equation of the form
\[L[n] = ax_{n+2} + bx_{n+1} + cx_n = f_n\]Let $x_h$ be general solution of $L[n] = 0$ and $x_p$ be a particular solution of $L[n] = f_n$. Then the general solution is
\[x_n = x_h + x_p\]
Similarily, $x_p$ involves some educated guess. Common cases are
| $f_n$ | $x_p$ |
| $a_k n^k + a_{k-} b^{k-1} + …$ | $b_k n^k + b_{k-1} n^{k-1} + …$ |
| $\lambda^n$ | $a \lambda^n$ |
In case $x_p$ is one of the solution in $x_h$, we can multiply it by $n$ or $n^2$ to form a new solution.
First Order + Nonlinear
Consider a general difference equation
\[x_{n+1} = f(x_n)\]Definition. A fixed point is a point $x^\ast$ such that
\[f(x^\ast) = x^\ast\]so that if $x_n = x^\ast$ then $x_{n+1} = x^\ast$.
Definition. A fixed point is stable if you stay close to it provided that you start sufficiently near, i.e. for any $\epsilon > 0$ there exists a $\delta > 0$ such that
\[|x_0 - x^\ast| < \delta \quad \implies \quad |f^n(x_0) - x^\ast| < \epsilon \; \text{ for all } \; n = 0, 1, 2, ...\]
Definition. A fixed point is attracting if there exists a $\delta > 0$ such that
\[|x_0 - x^\ast| < \delta \quad \implies \quad f^n(x_0) \to x^\ast \; \text{ as } \; n \to \infty\]
Definition. A fixed point is unstable if for all $\delta > 0$ there exists a $\epsilon > 0$ such that
\[|x_0 - x^\ast| < \delta \quad \text{but} \quad |f^n(x_0) - x^\ast| > \epsilon \; \text{ for some } \; n > 0\]
Proposition. Analytically, suppose that $x_n = x^\ast + \delta_n$ where $\delta_n$ is small, then by Taylor series expansion
\[\begin{align*} x_{n+1} &= f(x^\ast + \delta_n) \\ &\approx f(x^\ast) + f'(x^\ast)\delta_n \\ &= x^\ast + f'(x^\ast)\delta_n \end{align*}\]We therefore have $\delta_{n+1} \approx f’(x^\ast)\delta_n$ and the solution is
\[\delta_n = [f'(x^\ast)]^n \delta_0\]Hence, $x^\ast$ is stable and attracting if $\vert f’(x^\ast) \vert < 1$ and unstable if $\vert f’(x^\ast) \vert > 1$.
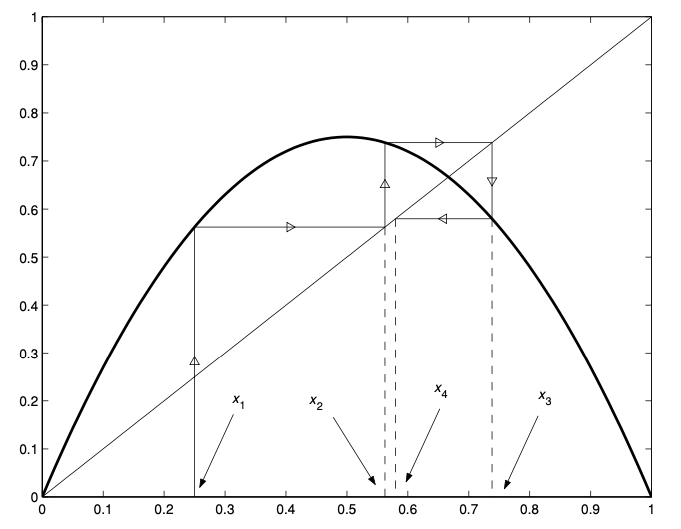
Graphically, we can produce a picture known as cobweb diagram by drawing $y = f(x)$ and the line $y = x$. Given $x_n$, we can find $x_{n+1}$ by drawing a line up to $f(x_n)$ then over to $y = x$, and repatedly to find $x_{n+2}, …$.
References
- James C. Robinson An Introduction to Ordinary Differential Equations, 2004 - Chapter 22, 23