Directional Derivatives
Directional derivatives are the generalization of partial derivatives for obtaining rate of change on an arbitrary direction.
Definition. The directional derivative of $f$ at $(x_0, y_0)$ in the direction of a unit vector $\mathbf{u} = (a, b)$ is
\[D_\mathbf{u} f(x_0, y_0) = \lim_{h \to 0} {f(x_0 + ha, y_0 + hb) - f(x_0, y_0) \over h}\]if this limit exists.
If $\mathbf{u} = \mathbf{i} = (1, 0)$, then $D_\mathbf{i} f = f_x$. If $\mathbf{u} = \mathbf{j} = (0, 1)$, then $D_\mathbf{j} f = f_y$.
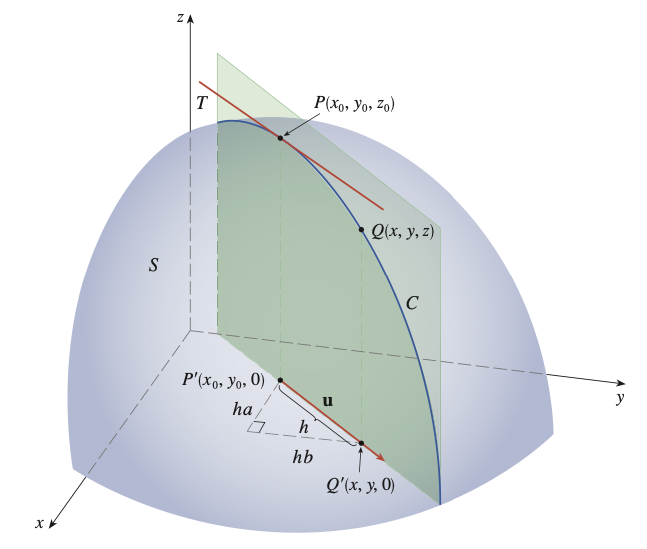
Theorem. If $f$ is a differentiable function of $x$ and $y$, then $f$ has a directional derivative in the direction of any unit vector $\mathbf{u} = (a, b)$ and
\[D_\mathbf{u} f(x, y) = f_x(x, y)a + f_y(x, y)b\]Alternatively, if $\mathbf{u} = (\cos \theta, \sin \theta)$, then $D_\mathbf{u} f(x, y) = f_x(x, y)\cos\theta + f_y(x, y)\sin\theta$.
Proof.
If we define a function $g$ of the single variable $h$ by
\[g(h) = f(x_0 + ha, y_0 + hb)\]then, by the definition of a derivative, we have
\[\begin{align*} g'(0) &= \lim_{h \to 0} {g(h) - g(0) \over h} = \lim_{h \to 0} { f(x_0 + ha, y_0 + hb) - f(x_0, y_0) \over h} \\ &= D_\mathbf{u} f(x_0, y_0) \end{align*}\]On the other hand, we can write $g(h) = f(x, y)$, where $x = x_0 + ha$, $y = y_0 + hb$, so
\[g'(h) = {\partial f \over \partial x} {\mathrm{d} x \over \mathrm{d} h} + {\partial f \over \partial y} {\mathrm{d} y \over \mathrm{d} h} = f_x(x, y)a + f_y(x, y)b\]If we put $h = 0$, then $x = x_0$ and $y = y_0$ and
\[g'(0) = f_x(x_0, y_0)a + f_y(x_0, y_0)b\]Hence,
\[D_\mathbf{u} f(x_0, y_0) = f_x(x_0, y_0)a + f_y(x_0, y_0)b\]
Gradient Vector
Definition. The gradient of $f$, denoted by $\nabla f$, is the vector function defined by
\[\nabla f(x, y) = (f_x(x, y), f_y(x, y))\]
Corollary. The directional derivative is the dot product of the gradient of $f$ and the unit vector, i.e.
\[D_\mathbf{u} f(x, y) = \nabla f(x, y) \cdot \mathbf{u}\]
We can also have $\mathbf{x} = (x, y)$ and write
\[D_\mathbf{u} f(\mathbf{x}) = \lim_{h \to 0} {f(\mathbf{x} + h\mathbf{u}) - f(\mathbf{x}) \over h} = \nabla f(\mathbf{x}) \cdot \mathbf{u}\]and generalize that for higher dimentions.
Theorem. The maximum value of the directional derivative $D_\mathbf{u}f(\mathbf{x})$ is $\vert \nabla f(\mathbf{x}) \vert$ and it occurs when $\mathbf{u}$ has the same direction as the gradient vector.
Proof.
\[D_\mathbf{u} f = \nabla f \cdot \mathbf{u} = \vert \nabla f \vert \cos \theta\]
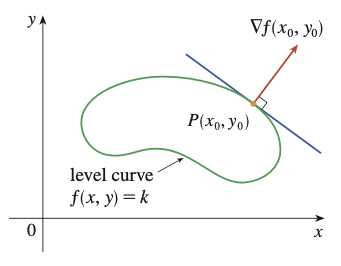
Proposition. Geometrically, suppose $S$ is a level curve with equation $f(x, y) = k$. Then $\nabla f(\mathbf{x})$ points in the direction of maximum rate of increase of $f$ at $\mathbf{x}$, i.e. perpendicular to the level curve or level surface of $f$ through $\mathbf{x}$.
Stationary Points
One of the application of derivatives is finding maximum and minimum values. Similarily,
Theorem. If $f$ has a local maximum/minimum at $(a, b)$, then $f_x(a, b) = 0$ and $f_y(a, b) = 0$.
Proof.
Let $g(x) = f(x, b)$. If $f$ has a local maximum/minimum at $(a, b)$, then $g$ as well at $a$, so $g’(a) = f_x(a, b) = 0$, and we can apply similar argument for $h(y) = f(a, y)$.
Similar to single-variable derivative, the converse is not necessary true.
Definition. A critical/stationary point is a point $(a, b)$ of $f$ such that $f_x(a, b) = 0$ and $f_y(a, b) = 0$. If the point is neither a local maximum/minimum, then it is called a saddle point.
Proposition. [Second Derivative Test] Let
\[D(a, b) = \begin{vmatrix} f_{xx} & f_{xy} \\ f_{yx} & f_{yy}\end{vmatrix}(a, b) = f_{xx}(a, b)f_{yy}(a, b) - [f_{xy}(a, b)]^2\]
If $D > 0$ and $f_{xx}(a, b) > 0$, then $f(a, b)$ is a local minimum.
If $D > 0$ and $f_{xx}(a, b) < 0$, then $f(a, b)$ is a local maximum.
If $D < 0$ then $f(a, b)$ is a saddle point.
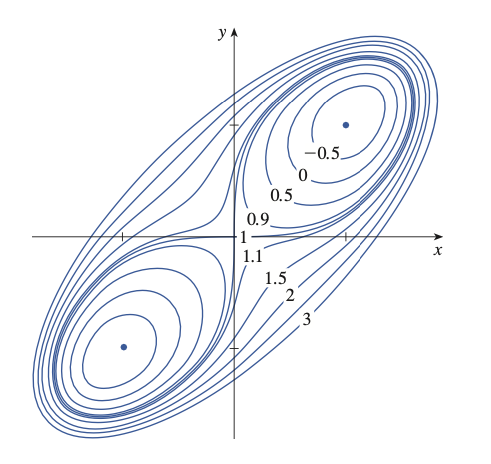
Here is an example contour map of $f(x, y) = x^4 + y^4 - 4xy + 1$. From that we can see $(1, 1)$ and $(-1, -1)$ are local maximum/minimum and $(0, 0)$ is a saddle point.
References
- James Stewart Single Variable Calculus, 2015 - Chapter 14