Laplace Transform

Definition. An integral transform is a relation of the form

\[F(s) = \int_\alpha^\beta K(s, t)f(t) \mathrm{d}t\]

where $K(s, t)$ is a given function, called the kernel of the transformation, and the limits of integration $\alpha$ and $\beta$ are also given.

Definition. [Laplace Transform] Let $f(t)$ be given fo $t \ge 0$. Then the Laplace transform of $f$ is defined by

\[\mathcal{L}\{f(t)\} = F(s) = \int_0^\infty e^{-st}f(t)\mathrm{d}t\]

whenever this improper integral converges.

Theorem. Suppose $f$ is piecewise continuous and $\vert f(t) \vert \le Ke^{at}$ when $t \ge M$. Then the Laplace transform $\mathcal{L}\{f(t)\}$ exists for $s > a$.

The Laplace transform of some important elementary functions are given in the following examples

Example. Let $f(t) = 1$, $t \ge 0$. Then

\[\mathcal{L}\{1\} = \int_0^\infty e^{-st} \mathrm{d}t = - \lim_{A \to \infty} \left[{e^{-st} \over s}\right]_0^A = {1 \over s}, \quad s > 0\]

Example. Let $f(t) = e^{at}$, $t \ge 0$. Then

\[\mathcal{L}\{e^{at}\} = \int_0^\infty e^{-(s - a)t} \mathrm{d}t = - \lim_{A \to \infty} \left[{e^{-(s - a)t} \over s - a}\right]_0^A = {1 \over s - a}, \quad s > a\]

Example. Let $f(t) = \sin at$, $t \ge 0$. Then

\[\mathcal{L}\{\sin at\} = {a \over a^2 + s^2}, \quad s > 0\]

Proposition. The Laplace transform is a linear operator, i.e.

\[\mathcal{L}\{\alpha f_1(t) + \beta f_2(t) \} = \alpha \mathcal{L}\{f_1(t)\} + \beta \mathcal{L}\{f_2(t)\}\]

Theorem. Suppose that $f$ is continuous and $f’$ is piecewise continuous. Then

\[\mathcal{L}\{f'(t)\} = s \mathcal{L}\{f(t)\} - f(0)\]

Proof.

Let $f’$ has $n$ points of discontinuity at $t_i$ and $t_0 = 0$ and $t_{n+1} = \infty$. By definition,

\[\mathcal{L}\{f'(t)\} = \int_0^\infty e^{-st}f'(t)\mathrm{d}t = \sum_{i=0}^{n} \left[ e^{-st}f(t) \right]_{t_i}^{t_{i+1}} + s\int_0^\infty e^{-st}f(t)\mathrm{d}t\]

As $f$ is continuous,

\[\sum_{i=0}^{n} \left[ e^{-st}f(t) \right]_{t_i}^{t_{i+1}} = \left[ e^{-st}f(t) \right]_0^\infty = -f(0)\]

Hence,

\[\mathcal{L}\{f'(t)\} = s \mathcal{L}\{f(t)\} - f(0)\]

Corollary. Suppose that $f’$ is continuous and $f’’$ is piecewise continuous. Then

\[\mathcal{L}\{f''(t)\} = s^2 \mathcal{L}\{f(t)\} - sf(0) - f'(0)\]

In general,

\[\mathcal{L}\{f^{(n)}(t)\} = s^n \mathcal{L}\{f(t)\} - s^{n-1}f(0) - \cdots - sf^{(n-2)}(0) - f^{(n-1)}(0)\]

The Laplace transform is useful for solving differential equations as it reduces the problem to an algebraic equation.

Heaviside Functions

Definition. The unit step function or Heaviside function, denoted by $u_c$, is defined by

\[u_c(t) = \begin{cases} 0 & t < c, \\ 1 & t \ge c, \end{cases} \quad c \ge 0\]

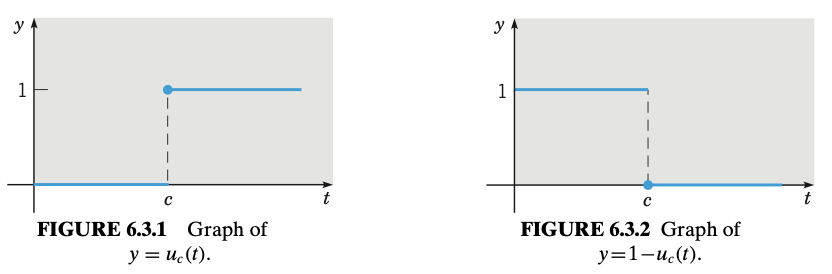
Theorem. If $F(s) = \mathcal{L}\{f(t)\}$ exists for $s > a \ge 0$ and if $c$ is a positive constant, then

\[\mathcal{L}\{u_c(t)f(t - c)\} = e^{-cs}\mathcal{L}\{f(t)\} = e^{-cs}F(s), \quad s > a\]

Conversely, if $f(t) = \mathcal{L}^{-1}\{F(s)\}$, then

\[u_c(t)f(t - c) = \mathcal{L}^{-1}\{e^{-cs}F(s)\}\]

Proof.

\[\begin{align*} \mathcal{L}\{u_c(t)f(t - c)\} &= \int_0^\infty e^{-st}u_c(t)f(t - c) \mathrm{d}t \\ &= \int_c^\infty e^{-st}f(t - c) \mathrm{d}t \\ &= \int_0^\infty e^{-s(\tilde{t} + c)} f(\tilde{t}) \mathrm{d}\tilde{t} \\ &= e^{-cs} \mathcal{L}\{f(t)\} \end{align*}\]

Corollary. By taking $f(t) = 1$, we have

\[\mathcal{L}(u_c(t)) = { e^{-cs} \over s}\]

A sketch of $y = u_c(t)f(t - c)$ is like this:

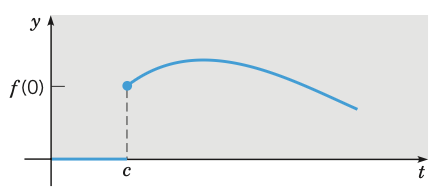
Theorem. If $F(s) = \mathcal{L}\{f(t)\}$ exists for $s > a \ge 0$ and if $c$ is a constant, then

\[\mathcal{L}\{e^{ct}f(t)\} = F(s - c), \quad s > a + c\]

Conversely, if $f(t) = \mathcal{L}^{-1}\{F(s)\}$, then

\[e^{ct}f(t) = \mathcal{L}^{-1}\{F(s - c)\}\]

Proof.

\[\begin{align*} \mathcal{L}\{e^{ct}f(t)\} &= \int_0^\infty e^{-(s-c)t}f(t) \mathrm{d}t \\ &= \int_0^\infty e^{-\tilde{s}t}f(t) \mathrm{d}t \\ &= F(\tilde{s}) = F(s - c) \end{align*}\]

Impulse Functions

In some physical systems, we have to deal with phenomena of an impulsive nature, e.g. voltage or bouncing ball.

Consider the function

\[d_\tau(t) = \begin{cases} 1/2\tau & -\tau < t < \tau \\ 0 & t \le -\tau \text{ or } t \ge \tau \\ \end{cases}\]

in which $\tau$ is a small positive constant. To idealize the forcing function $d_\tau$, we make it acting in a shorter and shorter time interval, i.e.

\[\lim_{\tau \to 0} d_\tau(t) = 0\]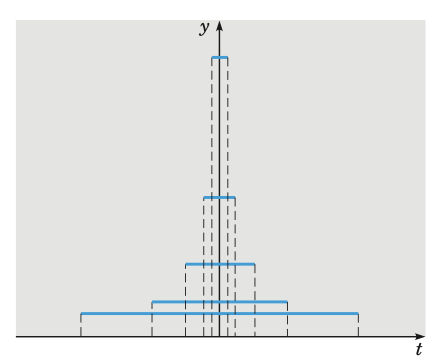

On the other hand, the total impulse by the forcing function is the integral

\[I(\tau) = \int_{-\infty}^\infty d_\tau(t)\mathrm{d}t\]

As long as $\tau \not = 0$, we have $I(\tau) = 1$. Therefore,

\[\lim_{\tau \to 0} I(\tau) = 1\]

Definition. A unit impulse function or Dirac delta function, denoted by $\delta(t)$, is defined by

\[\delta(t) = 0, t \not= 0 \quad \text{and} \quad \int_{-\infty}^\infty \delta(t) \mathrm{d}t = 1\]

A unit impulse at $t = t_0$ is therefore given by

\[\delta(t - t_0) = 0, t \not= t_0 \quad \text{and} \quad \int_{-\infty}^\infty \delta(t - t_0) \mathrm{d}t = 1\]

Proposition. The Laplace transform of $\delta(t - t_0)$ is

\[\mathcal{L}\{\delta(t - t_0)\} = e^{-st_0}\]

Hence, we have

\[\mathcal{L}\{\delta(t)\} = \lim_{t_0 \to 0} e^{-st_0} = 1\]

Proof.

Consider the Laplace transform of $d_\tau(t - t_0)$, we have

\[\begin{align*} \mathcal{L}\{d_\tau(t - t_0)\} &= \int_0^\infty e^{-st}d_\tau(t - t_0) \mathrm{d}t \\ &= \int_{t_0 - \tau}^{t_0 + \tau} e^{-st}d_\tau(t - t_0) \mathrm{d}t \\ &= {1 \over 2\tau} \int_{t_0 - \tau}^{t_0 + \tau} e^{-st} \mathrm{d}t \\ &= -{1 \over 2s\tau} \left[ e^{-st} \right]_{t_0 - \tau}^{t_0 + \tau} \\ &= {1 \over s\tau} \left( {e^{s\tau} - e^{-s\tau} \over 2} \right) e^{-st_0} \\ &= {\sin s\tau \over s\tau} e^{-st_0} \end{align*}\]

By definition of $\delta(t - t_0)$, we have

\[\begin{align*} \mathcal{L}\{\delta(t - t_0)\} &= \lim_{\tau \to 0} \mathcal{L}\{d_\tau(t - t_0)\} \\ &= \lim_{\tau \to 0} {\sin s\tau \over s\tau} e^{-st_0} \\ &= e^{-st_0} \end{align*}\]

Proposition. The integral of the product of delta function and any continuous function $f$ is

\[\int_{-\infty}^\infty \delta(t - t_0)f(t)\mathrm{d}t = f(t_0)\]

Proof.

By the definition of delta function and mean value theorem for integrals, we have

\[\begin{align*} \int_{-\infty}^\infty \delta(t - t_0)f(t)\mathrm{d}t &= \lim_{\tau \to 0} \int_{-\infty}^\infty d_\tau(t - t_0)f(t)\mathrm{d}t \\ &= \lim_{\tau \to 0} {1 \over 2\tau} \int_{t_0 - \tau}^{t_0 + \tau} f(t)\mathrm{d}t \\ &= \lim_{\tau \to 0} {1 \over 2\tau} 2\tau \cdot f(t^\ast) \\ &= \lim_{\tau \to 0} f(t^\ast) \end{align*}\]

As $t_0 - \tau < t^\ast < t_0 + \tau$ and $\tau \to 0$, $t^\ast \to t_0$. Hence,

\[\int_{-\infty}^\infty \delta(t - t_0)f(t)\mathrm{d}t = f(t_0)\]

There is a subtle relationship between the Dirac delta function and Heaviside function.

Proposition. The Heaviside function can be defined by

\[u_0(x) = H(x) = \int_{-\infty}^x \delta(t) \mathrm{d}t\]

Hence, by the F.T.C.,

\[{\mathrm{d}H \over \mathrm{d}x} = \delta(x)\]

References

• William E. Boyce Elementary Differential Equations and Boundary Value Problems, 2009 - Chapter 6