Polyhedral Groups
The polyhedral groups are the symmetrices of the five platonic solids.

| Solid | Polygon | Faces | Vertices | Edges |
| Tetrahedron | Triangle | 4 | 4 | 6 |
| Cube | Square | 6 | 8 | 12 |
| Octahedron | Triangle | 8 | 6 | 12 |
| Dodecahedron | Pentagon | 12 | 20 | 30 |
| Icosahedron | Triangle | 20 | 12 | 30 |
Cube
Proposition. Let $G^{+}$ be the group of all rotations of a cube, acting on the vertices. Then
\[|G^{+}| = 24\]Proof.
Choose a vertex as $1$. As the action is transitive, $|\text{orb}(1)| = 8$. The rotations that fixes $1$ are those in the axis through $1$ and the diagonally opposite vertex, so there are three of them and $|\text{Stab}(1)| = 3$.
Hence,
\[|G^{+}| = |\text{orb}(1)| \cdot |\text{Stab}(1)| = 8 \cdot 3 = 24\]
Proposition. $G^{+} \cong S_4$.
Proof.
Consider $G^{+}$ acting on the four diagonal of the cube, which gives a homomorphism $\varphi: G^{+} \to S_4$. The rotation around axis through the top and bottom face gives $(1\;2\;3\;4) \in \text{im}\,\varphi$. The rotation around axis thorugh the mid point of edge containing $1$ and $2$ gives $(1\;2) \in \text{im}\,\varphi$. As $\Set{(1\;2), (1\;2\;3\;4)}$ generates $S_4$, $\text{im}\,\varphi = S_4$, i.e. $\varphi$ is surjective. But $|G^{+}| = |S_4| = 24$, $\varphi$ is an isomorphism.
Proposition. The group $G$ of all symmetries of the cube is isomorphic to $S_4 \times C_2$.
Proof.
Let $G$ acts on the vertices of the cube. Similarily, $|\text{orb}(1)| = 8$. The stablizer of $1$ is the identity, two rotations in axis through $1$ and three reflections through $1$ and edge coming out of $1$, so $|\text{Stab}(1)| = 6$. Thus, $|G| = 48$.
The “reflection in midpoint” $\tau$ is the symmetry that commutes with all other symmetries. Also, $G^{+} \cap \tau = \Set{e}$. So
\[\varphi: G^{+} \times \langle \tau \rangle \to G, (g, h) \mapsto gh\]is an injective homomorphism. It is also surjective as $|G| = |S_4 \times C_2|$. Hence, $G \cong S_4 \times C_2$.
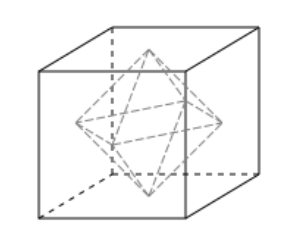
Octahedron
Proposition. The group $G$ of all symmetries of the octahedron is isomorphic to $S_4 \times C_2$.
Proof.
Put each vertex of the octahedron on the centre of a face of the cube, and vice versa, the group of symmetries is isomorphic to that of cube.
Tetrahedron
Proposition. Let $G^{+}$ be the group of all rotations of a tetrahedron, acting on the vertices. Then
\[|G^{+}| = 12\]Proof.
Choose a vertex as $1$. As the action is transitive, $|\text{orb}(1)| = 4$. The rotations that fixes $1$ is those in the axis through $1$ and the centre of opposite face, so there are three of them and $|\text{Stab}(1)| = 3$.
Hence,
\[|G^{+}| = |\text{orb}(1)| \cdot |\text{Stab}(1)| = 4 \cdot 3 = 12\]
Proposition. $G^{+} \cong A_4$.
Proof.
We have
\[\begin{align*} (2\;3\;4), (2\;4\;3) &\in \text{Stab}(1) \\ (1\;3\;4), (1\;4\;3) &\in \text{Stab}(2) \\ (1\;2\;4), (1\;4\;2) &\in \text{Stab}(3) \\ (1\;2\;3), (1\;3\;2) &\in \text{Stab}(4) \\ \end{align*}\]Also, the rotations in axes through midpoints of opposite edges give $(1\;2)(3\;4), (1\;4)(2\;3), (1\;3)(2\;4)$. Hence, $G^{+} \cong A_4$.
Proposition. The group $G$ of all symmetries of the tetrahedron is isomorphic to $S_4$.
Proof.
Let $G$ acts on the vertices of the tetrahedron, a homomorphism $\phi: G \to S_4$. If all four vertices are fixed, the whole tetrahedron is fixed, so $\ker \phi = \Set{e}$ and $\phi$ is injective.
The reflection throught $1$ and $2$ swaps $3$ and $4$, so
\[\text{Stab}(1) = \langle (2\;3\;4), (3\;4) \rangle \cong D_6\]Therefore, $|G| = 4 \cdot 6 = 24$ and $\phi$ is surjective. Hence, $\phi$ is an isomorphism and $G \cong S_4$.