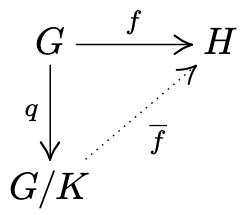Quotient Groups
The theory about quotient groups is one of the most important idea about groups.
Normal Subgroups
Definition. A subgroup $K$ of $G$ is a normal subgroup if for all $a \in G$ and for all $k \in K$, we have $aka^{-1} \in K$. It is denoted by $K \trianglelefteq G$.
Proposition. $K \trianglelefteq G \iff \forall a \in G, aK = Ka$.
Proof.
($\Leftarrow$) If the left cosets of $K$ are equal to its right cosets, for all $a \in G$ and some $k, k’ \in K$, we have
\[\begin{align*} ak &= k'a \\ aka^{-1} &= k' \end{align*}\]so $aka^{-1} \in K$ and $K \trianglelefteq G$.
($\Rightarrow$) If $K \trianglelefteq G$, for all $a \in G$ and $k \in K$, $aka^{-1} \in K$, we have $aka^{-1} = k’$ for some $k’ \in K$ so $ak = k’a$ and $aK \subseteq Ka$. Also, we have $a^{-1}k(a^{-1})^{-1} = a^{-1}ka = k’$ for some $k’ \in K$, so $ka = ak’$ and $Ka \subseteq aK$. Hence, $aK = Ka$.
Proposition. $K \trianglelefteq G \iff \forall a \in G, aKa^{-1} = K$.
Proof.
($\Leftarrow$) If for all $a \in G$, $aKa^{-1} = K$, then for all $k \in K$, $aka^{-1} = k’$ for some $k’ \in K$. By definition, $K \trianglelefteq G$.
($\Rightarrow$) If $K \trianglelefteq G$, for all $a \in G$ and $k \in K$, $aka^{-1} \in K$, we have $aka^{-1} \in K$ so $aKa^{-1} \subseteq K$. Also, we have $a^{-1}ka \in K$, so $a(a^{-1}ka)a^{-1} = k \in aKa^{-1}$ and $K \subseteq aKa^{-1}$. Hence, $aKa^{-1} = K$.
Proposition. Any subgroup of index $2$ is normal.
Proof.
If $K \le G$ is of index $2$, the only possible cosets are $K$ and $G \setminus K$ because $eK$/$Ke$ is one of the cosets and cosets are disjoint. As $eK = Ke$, the other right coset is also $G \setminus K$. So the left cosets and right cosets of $K$ are the same and $K \trianglelefteq G$.
Proposition. Any subgroup of an abelian group is normal.
Proof.
For a subgroup $K \le G$, for all $a \in G$ and $k \in K$, $aka^{-1} = aa^{-1}k = k \in K$. Also, as $K$ is abelian, obviously $aK = Ka$ for all $a \in G$.
Definition. A group $G$ is simple if it has no non-trivial proper normal subgroups (i.e. only $\set{e}$ and G).
Quotients
The left cosets of normal subgroups form a group in a natural way.
Definition. If $A$ and $B$ are subsets of $G$, the product $AB$ is the set of all products $ab$ where $a \in A$ and $b \in B$.
Lemma. The product of two left cosets of a normal subgroup is again a left coset, i.e.
\[(aK)(bK) = abK\]Proof.
Each element of $(aK)(bK)$ has the form $akbk’$ for some $k, k’ \in K$. Rewrite this as
\[ab(b^{-1}kb)k'\]As $K$ is a normal subgroup, by definition, $b^{-1}kb = k’’ \in K$. Hence,
\[akbk' = ab(b^{-1}kb)k' = ab(k''k')\]and therefore $(aK)(bK) \subseteq abK$.
Conversely, for any $abk \in abK$, $abk = (ae)(bk) \in (aK)(bK)$. Hence, $abK \subseteq (aK)(bK)$.
Theorem. If $K$ is a normal subgroup of $G$, the set of all left cosets of $K$ in $G$ forms a group under multiplication.
Proof.
The above lemma shows that the multiplication of left cosets is closed. $(eK)(aK) = aK$ is the identity element. $(a^{-1}K)(aK) = eK$ so $a^{-1}K$ is the inverse of $aK$. Associativity is inherited from associativity in $G$. Hence, it is a group.
Definition. The quotient group (or factor group) of $G$ by $K$ is the group of left cosets of $K$ under multiplication, denoted by $G/K$.
Isomorphism Theorem
The isomorphism theorem is about the relationship between normal subgroups, quotients and homomorphisms.
Lemma. Every normal subgroup is the kernel of some homomorphisms, specifically, given $K \trianglelefteq G$, the map $q: G \to G/K$ sending $a$ to $aK$ is a surjective group homomorphism, called the quotient map.
Proof.
By definition,
\[q(ab) = abK = (aK)(bK) = q(a)q(b)\]so $q$ is a homomorphism. $G/K$ is the group of all left cosets of $K$ so clearly $q$ is surjective.
Lemma. Every kernel of homomorphisms is a normal subgroup.
Proof.
Let $f: G \to H$ be a homomorphism, $K = \ker f$ are the elements $k \in G$ such that $f(k) = e_H$. Therefore, for all $a \in G$, $f(aka^{-1}) = f(a)f(k)f(a^{-1}) = f(a)f(a)^{-1} = e_H$, so $aka^{-1} \in K$ and $\ker f \trianglelefteq G$.
We have already shown that the image of a homomorphism is a subgroup. Furthermore,
Theorem. [Isomorphism Theorem] The image of a homomorphism $f: G \to H$ is isomorphic to the quotient group $G/K$, where $K = \ker f$, i.e. $\text{im}\,f \cong G/K$.
Proof.
Define $\bar{f}: G/K \to H$ by $\bar{f}(aK) = f(a)$ (so that $\bar{f}q = f$).
If $aK = bK$, we have $b^{-1}a \in K$, so $f(b^{-1}a) = f(b)^{-1}f(a) = e$ and $f(a) = f(b)$. Therefore, $aK = bK \implies \bar{f}(aK) = \bar{f}(bK)$ so $\bar{f}$ is well-defined.
If $\bar{f}(aK) = \bar{f}(bK)$, we have $f(a) = f(b) \implies f(b^{-1}a) = e$ and $b^{-1}a \in K$. Therefore, $aK = bK$ and $\bar{f}$ is injective.
By definition, $\bar{f}$ is clearly surjective onto $\text{im}\,f$.
So, $\bar{f}$ is an isomorphism and $G/K \cong \text{im}\,f$ ($\le H$).
In particular, if $f: G \to H$ is injective, then $\ker f = \set{e}$ (injectivity via kernel), so $G/K \cong G$ and $G$ is isomorphic to a subgroup of $H$, denoted by $G \lesssim H$. If $f: G \to H$ is surjective, then $\text{im} f = H$, so $G/K \cong H$.