Green’s and Stokes’ Theorems
We continue our discussion of theorems that reduce higher order integral to a lower order one just like the divergence theorem. Two of the important ones are Green’s Theorem and Stokes’ Theorem.
Green’s Theorem
Green’s Theorem is equivalent to the 2D Divergence Theorem which focuses more on actual evaluation of the integral.
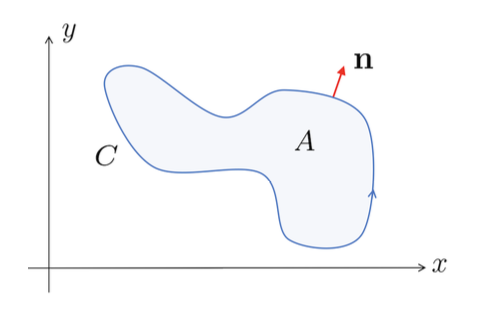
Theorem. [Green’s Theorem] Let $P(x, y)$ and $Q(x, y)$ be smooth functions on $\mathbb{R}^2$. Then
\[\int_A \left( {\partial Q \over \partial x} - {\partial P \over \partial y} \right) \,dA = \oint_C P \,dx + Q \,dy\]where $A$ is a bounded region in the plane and $C = \partial A$ is a piecewise smooth, non-intersecting closed curve which is traversed anti-clockwise.
Proof.
Let $\mathbf{F} = (Q, -P)$ be a vector field in $\mathbb{R}^2$. We then have
\[\int_A \nabla \cdot \mathbf{F} \,dA = \int_A \left( {\partial Q \over \partial x} - {\partial P \over \partial y} \right) \,dA\]Let $\mathbf{x}(s) = (x(s), y(s))$ be the parameterisation of $C$. Then the normal vector
\[\mathbf{n} = (y'(s), -x'(s))\]which points outward provided that the arc length $s$ increases in the anti-clockwise direction.
We then have
\[\mathbf{F} \cdot \mathbf{n} = Q {dy \over ds} + P {dx \over ds}\]and so the integral is
\[\int_C \mathbf{F} \cdot \mathbf{n} \,ds = \int_C P \,dx + Q \,dy\]By divergence theorem, the L.H.S of the two equations are equal and so as the R.H.S.
Stokes’ Theorem
Stokes’ Theorem is an extension of Green’s Theorem, where the surface is no longer restricted to lie in a plane.
Theorem. [Stokes’ Theorem] Let $S$ be a smooth surface in $\mathbb{R}^3$ parameterised by $\mathbf{r}$ with a piecewise smooth curve $C = \partial S$ as boundary. For any smooth vector field $\mathbf{F}$, we have
\[\int_S \nabla \times \mathbf{F} \cdot d\mathbf{S} = \oint_C \mathbf{F} \cdot d\mathbf{r}\]Proof.
For a surface $S$ parameterised by $\mathbf{r}(u, v)$, we have
\[d\mathbf{S} = \left( { \partial \mathbf{r} \over \partial u } \times { \partial \mathbf{r} \over \partial v } \right) \,du \,dv\]Therefore, for a vector field $\mathbf{F}$, we have
\[\begin{align*} \nabla \times \mathbf{F} \cdot d\mathbf{S} &= \left( \varepsilon_{ijk} {\partial F_k \over \partial x_j} \right) \left( \varepsilon_{ipq} {\partial x_p \over \partial u} {\partial x_q \over \partial v} \right) \,du \,dv \\ &= (\delta_{jp}\delta_{kq} - \delta_{jq}\delta_{kp}) {\partial F_k \over \partial x_j} {\partial x_p \over \partial u} {\partial x_q \over \partial v} \,du \,dv \\ &= \left({\partial F_k \over \partial x_j} {\partial x_j \over \partial u} {\partial x_k \over \partial v} - {\partial F_k \over \partial x_j} {\partial x_k \over \partial u} {\partial x_j \over \partial v} \right) \,du \,dv \\ &= \left({\partial F_k \over \partial u} {\partial x_k \over \partial v} - {\partial F_k \over \partial v} {\partial x_k \over \partial u} \right) \,du \,dv \\ &= \left[{\partial \over \partial u} \left( F_k {\partial x_k \over \partial v} \right) - {\partial \over \partial v} \left( F_k {\partial x_k \over \partial u} \right) \right] \,du \,dv \end{align*}\]Hence,
\[\begin{align*} \int_S \nabla \times \mathbf{F} \cdot d\mathbf{S} &= \iint_A \left[{\partial \over \partial u} \left( F_k {\partial x_k \over \partial v} \right) - {\partial \over \partial v} \left( F_k {\partial x_k \over \partial u} \right) \right] \,du \,dv \\ &= \int_C F_k {\partial x_k \over \partial u} \,du + F_k {\partial x_k \over \partial v} \,dv \\ &= \oint_C F_k \,dx_k = \oint_C \mathbf{F} \cdot d\mathbf{r} \end{align*}\]where the second last line follows from Green’s Theorem with $P = F_k \partial_u x_k$ and $Q = F_k \partial_v x_k$.
The orientations of $\mathbf{S}$ and $\mathbf{C}$ should be compatible. If the surface has normals pointing upward, then the orientation of $C$ is anti-clockwise, i.e. $\mathbf{t} \times \mathbf{n}$ points out of $S$.
Stokes’ Theorem thus states that the flux of $\nabla \times \mathbf{F}$ across an open surface $S$ is equal to the circulation of $\mathbf{F}$ round the bounding curve $C$.
Stokes’ Theorem also gives us another intuition for the meaning of curl. By integrating $\nabla \times \mathbf{F}$ over a small enough surface such that $\nabla \times \mathbf{F}$ is approximately constant, we have
\[\int_S \nabla \times \mathbf{F} \cdot d\mathbf{S} \approx A \mathbf{n} \cdot (\nabla \times \mathbf{F})\]where $A$ is the area and $\mathbf{n}$ is the normal. By limiting the area $A$ to zero, we can conclude the following.
Corollary. The curl of a vector field $\mathbf{F}$ can be defined by
\[\mathbf{n} \cdot (\nabla \times \mathbf{F}) = \lim_{A \to 0} {1 \over A} \int_C \mathbf{F} \cdot d\mathbf{x}\]which is coordinate independent.
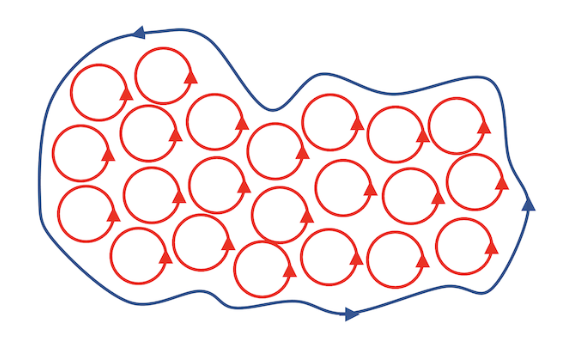
Geometrically, it means the value of $\nabla \times \mathbf{F}$ in the direction of $\mathbf{n}$ is the local circulation of $\mathbf{F}$ in the plane normal to $\mathbf{n}$. When we integrate this circulation over some surface $S$, most of it cancels out and the only thing that’s left is the circulation around the edge.
Corollary. A vector field is conservative iff the field is irrotational, i.e.
\[\mathbf{F} = \nabla \phi \iff \nabla \times \mathbf{F} = 0\]Proof.
($\Rightarrow$) As shown before, the curl of the gradient field is always zero, i.e. $\nabla \times (\nabla \phi) = 0$
($\Leftarrow$) Suppose that $\nabla \times \mathbf{F} = 0$. By Stokes’ Theorem, we have
\[\int_S \nabla \times \mathbf{F} \cdot d\mathbf{S} = \oint_C \mathbf{F} \cdot d\mathbf{x} = 0\]which is the definition of conservativity.
Corollary. For a smooth scalar field $\phi$, we have
\[\int_S \nabla \phi \times d\mathbf{S} = - \oint_C \phi \,d\mathbf{x}\]Proof.
Let $\mathbf{a}$ be an arbitrary vector and $\mathbf{F} = \mathbf{a} \phi$, then
\[\int_S \nabla \times (\mathbf{a} \phi) \cdot d\mathbf{S} = \oint_C \phi \mathbf{a} \cdot d\mathbf{x} = \mathbf{a} \cdot \oint_C \phi d\mathbf{x}\]But
\[\begin{align*} \nabla \times (\mathbf{a} \phi) \cdot d\mathbf{S} &= \left( \varepsilon_{ijk} { \partial a_k \phi \over \partial x_j } \right) n_i \,dS \\ &= a_k \left( \varepsilon_{kij} \,n_i { \partial \phi \over \partial x_j } \right) \,dS \\ &= \mathbf{a} \cdot (\mathbf{n} \times \nabla \phi) \,dS \\ &= - \mathbf{a} \cdot (\nabla \phi \times \mathbf{n}) \,dS \end{align*}\]and hence
\[- \mathbf{a} \cdot \int_S \nabla \phi \times d\mathbf{S} = \mathbf{a} \cdot \oint_C \phi \,d\mathbf{x} \\\]and $\mathbf{a}$ is arbitrary so
\[\int_S \nabla \phi \times d\mathbf{S} = - \oint_C \phi \,d\mathbf{x}\]
References
- Stephen J. Cowley Vector Calculus Lectures Notes, 2000 - Chapter 6.2, 6.3
- David Tong Vector Calculus Lecture Notes, 2024 - Chapter 4.3, 4.4
- K.F. Riley Mathematical Methods for Physicists and Engineers, 1998 - Chapter 11.9