Line and Surface Integrals
It is often to consider the integration of scalar or vector fields along lines, over surfaces and throughout volumes.
Line Integrals
Definition. Line integral is the integration of some quantity related to a scalar/vector field between two given points, $A$ and $B$, in space along a prescribed curve $C$ that joins them. In general, they will be of the forms
\[\int_C \phi \,ds \qquad \int_C \mathbf{F} \cdot d\mathbf{s}\]where $\phi$ is a scalar field and $\mathbf{F}$ is a vector field. Both of the integrals are scalar in nature.
The formal definition is similar to that of ordinary integrals with the use of dissection and summing over the intervals.
Definition. If $C$ is closed, the line integral will be written as
\[\oint_C \phi \,ds \qquad \oint_C \mathbf{F} \cdot d\mathbf{s}\]
For a close curve we have to specify the direction around the loop in which the integral is taken. By convention, it is usually taken to be such that the region $R$ is on the left, i.e. anticlockwise if viewed from above.
Definition. The line integral of a scalar field $\phi(\mathbf{x}): \mathbb{R}^3 \to \mathbb{R}$ along the curve $C: \mathbf{r}(s)$ is defined to be
\[\int_C \phi(\mathbf{x}) \,ds = \int_{s_a}^{s_b} \phi(\mathbf{r}(s)) \,ds\]
The line integral is, by convention, defined so that $\int_C ds$ gives the length of the curve in which is positive.
Proposition. Suppose that the curve is parameterised by variable $u$ other than the arc length, by the rules governing the change of variable of Riemann integral,
\[\int_C \phi(\mathbf{x}) \,ds = \int_{s_a}^{s_b} \phi(\mathbf{r}(s)) \,ds = \int_{u_a}^{u_b} \phi(\mathbf{r}(u)) |\dot{\mathbf{r}}(u)| \,du\]
Definition. The scalar line integral of a vector field $\mathbf{F}(\mathbf{x}): \mathbb{R}^3 \to \mathbb{R}^3$ along the curve $C: \mathbf{r}(u)$ is defined to be
\[\int_C \mathbf{F} \cdot d\mathbf{s} = \int_C \mathbf{F} \cdot d\mathbf{r} = \int_{u_a}^{u_b} \mathbf{F}(\mathbf{r}(u)) \cdot {d \mathbf{r} \over du} \,du\]
The vector differential $d\mathbf{s}$ is just an alternative notation of $d\mathbf{r}$. It is a more generic and can be used to cater other coordinate systems.
Proposition. In Cartesian coordiante, since $d\mathbf{r} = d\mathbf{x} = (dx, dy, dz)$, we have
\[\int_C \mathbf{F} \cdot d\mathbf{x} = \int_C F_1 \,dx + F_2 \,dy + F_3 \,dz\]
Proposition. Similar to ordinary integrals,
\[\int_{-C} \phi \,ds = -\int_C \phi \,ds \qquad \int_C \phi \,ds = \int_{C_1} \phi \,ds + \int_{C_2} \phi \,ds\]and
\[\int_{-C} \mathbf{F} \cdot d\mathbf{s} = -\int_C \mathbf{F} \cdot d\mathbf{s} \qquad \int_C \mathbf{F} \cdot d\mathbf{s} = \int_{C_1} \mathbf{F} \cdot d\mathbf{s} + \int_{C_2} \mathbf{F} \cdot d\mathbf{s}\]
Definition. We can also define the vector line integral by evaluating component by component, i.e.
\[\int_C \phi \,d\mathbf{r} = \sum_{j=1}^3 \mathbf{e}_j \int \phi \,dx_j\]and
\[\int_C \mathbf{F} \,ds = \sum_{j=1}^3 \mathbf{e}_j \int_{s_a}^{s_b} F_j(\mathbf{r}(s)) \,ds\]or cross product, i.e.
\[\int_C \mathbf{F} \times d\mathbf{s}\]
Conservative Fields
In general, the value of a line integral between two points $A$ and $B$ depends on the path $C$ taken. However, there exists a class of vector fields for which the line integral is independent of the path taken. Such vector fields are called conservative.
Definition. A vector field $\mathbf{F}$ is conservative if there exists scalar field $\phi$ such that
\[\mathbf{F} = \nabla \phi\]
Definition. The scalar field $\phi$ is called the scalar potential function of the conservative vector field $\mathbf{F}$, and is unique up to an arbitrary additive constant.
Proposition. The line integral is independent of the path taken, i.e. the integral around any closed loop is zero, iff $\mathbf{F}$ is conservative.
Proof.
($\Leftarrow$) Suppose that $\mathbf{F} = \nabla \phi$. For any curve $C$ with parameterisation $\mathbf{r}(u)$, when we integrate $\mathbf{F}$ from $\mathbf{a}$ to $\mathbf{b}$, we have
\[\begin{align*} \int_C \mathbf{F} \cdot d\mathbf{r} = \int_C \nabla \phi \cdot d\mathbf{r} &= \int_{u_a}^{u_b} { \partial \phi \over \partial x^i } { d x^i \over du} \,du \\ &= \int_{u_a}^{u_b} { d \over du } \phi(\mathbf{r}(u)) \,du \\ &= \Bigl[ \phi(\mathbf{r}(u)) \Bigr]_{u_a}^{u_b} \\ &= \phi(\mathbf{b}) - \phi(\mathbf{a}) \end{align*}\]($\Rightarrow$) Given the line integral from $A$ to $B$ is independent of the path taken, its value must be a function only of the positions, i.e.
\[\int_A^B \mathbf{F} \cdot d\mathbf{r} = \phi(B) - \phi(A)\]If $A$ and $B$ are separated by an infinitesimal displacement $d\mathbf{r}$ then
\[\mathbf{F} \cdot d\mathbf{r} = d\phi\]Since $d\phi = \nabla \phi \cdot d\mathbf{r}$, $(\mathbf{F} - \nabla \phi) \cdot d\mathbf{r} = 0$ and hence $\mathbf{F} = \nabla \phi$.
This result is closely related to the fundamental theorem of calculus: the line integral of a conservative vector field is the analog of the integral of a total derivative and so is given by the end points.
Proposition. If $\mathbf{F}$ is a conservative field, then for any two components $F_i$ and $F_j$, we have $\partial_j F_i = \partial_i F_j$.
Alternatively, we can use differential to phrase the idea of a conservative vector field.
Definition. The differential of a function $\phi(\mathbf{r})$ on $\mathbb{R}^n$ is defined to be
\[d\phi = { \partial \phi \over \partial x^i } dx^i = \nabla \phi \cdot d\mathbf{r}\]
Definition. A differential is exact if it can be written as $\mathbf{F} \cdot d\mathbf{r} = d \phi$ for some scalar function $\phi$.
Corollary. A differential is exact iff the vector field is conservative.
Surface Integrals
Definition. Surface integral is the integration of some quantity related to a scalar/vector field over a surface. The common scalar surface integrals are of the forms
\[\int_S \phi \,dS \qquad \int_S \mathbf{F} \cdot d\mathbf{S}\]and vector surface integrals are of the forms
\[\int_S \phi \,d\mathbf{S} \qquad \int_S \mathbf{F} \,dS \qquad \int_S \mathbf{F} \times d\mathbf{S}\]where $\phi$ is a scalar field and $\mathbf{F}$ is a vector field and $dS$ and $d\mathbf{S}$ are the infinitesimal scalar and vector areas respectively.
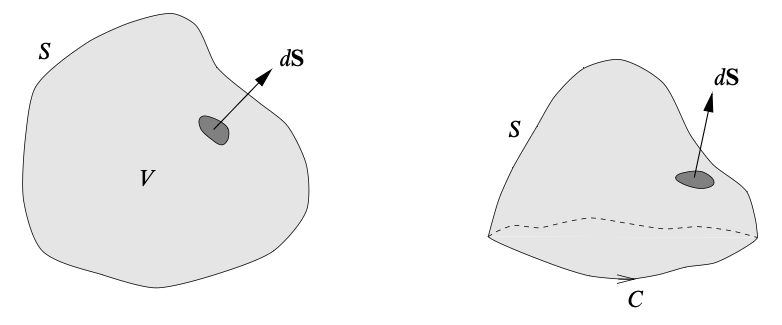
Definition. If $S$ is closed, the surface integral will be written as, for example,
\[\oint_S \mathbf{F} \cdot d\mathbf{S}\]
Definition. For closed surface, the vector differential $d\mathbf{S}$ of the surface $S$ has direction pointing outwards. For open surface, it is given by the right-hand sense with respect to the direction in which the perimeter is traversed.
Definition. Suppose that $\phi$ is a scalar field and $S$ is a surface parameterised by $\mathbf{r}(u, v)$. Then the surface integral is given by
\[\int_S \phi(\mathbf{r}) \,dS = \iint_R du\,dv \left| {\partial \mathbf{r} \over \partial u} \times {\partial \mathbf{r} \over \partial v} \right| \phi(\mathbf{r})\]
Definition. Suppose that $\mathbf{F}$ is a vector field and $S$ is a surface parameterised by $\mathbf{r}(u, v)$. Then the scalar surface integral is given by
\[\int_S \mathbf{F}(\mathbf{r}) \cdot d\mathbf{S} = \int_S \mathbf{F}(\mathbf{r}) \cdot \mathbf{n} \,dS = \iint_R du\,dv \left( {\partial \mathbf{r} \over \partial u} \times {\partial \mathbf{r} \over \partial v} \right) \cdot \mathbf{F}(\mathbf{r})\]This is called the flux of $\mathbf{F}$ through $S$.
The physical importance of the flux can be seen by thinking about a fluid. Let $\mathbf{F}(\mathbf{x})$ be the velocity field of a fluid. In a small time $\Delta t$, the amount of fluid flowing through a small surface element $\Delta S$ is given by
\[\text{Flow} = \mathbf{F} \Delta t \cdot \mathbf{n} \Delta S\]Integrating over the whole surface, we have
\[\text{Flux} = {\text{Flow} \over \text{Time}} = \int_S \mathbf{F} \cdot d\mathbf{S}\]which is the amount of fluid crossing $S$ per unit time, i.e. the rate of fluid flow.
Proposition. Surface integral is independent of the choice of parameterisation of the surface.
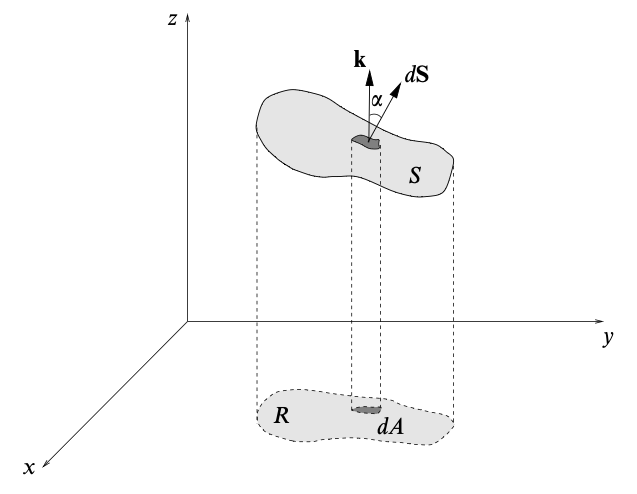
Sometimes, it is not possible to represent the surface in a simple way in any particular coordinate system (i.e. cannot be parameterised). In such cases, we have to consider the projections of the surface onto the Cartesian coordinate planes.
Proposition. Suppose that $S$ is a surface given by the equation $f(x, y, z) = 0$, then
\[dS = {|\nabla f| \over \partial f / \partial z} dA\]Proof.
The unit normal at any point of the surface is given by $\mathbf{n} = \nabla f / \vert \nabla f \vert$.
Hence,
\[dS = {dA \over |\cos \alpha|} = {dA \over |\mathbf{n} \cdot \mathbf{k}|} = { |\nabla f| \,dA \over \nabla f \cdot \mathbf{k} } = {|\nabla f| \over \partial f / \partial z} dA\]
Definition. The vector area of a surface $S$ is defined as
\[\mathbf{S} = \int_S d\mathbf{S}\]
Volume Integrals
Definition. Volume integral is the integration of some quantity related to a scalar/vector field throughout a volume. In general, they will be of the forms
\[\int_V \phi \,dV \qquad \int_V \mathbf{F} \,dV\]where $\phi$ is a scalar field and $\mathbf{F}$ is a vector field. The integrals themselves are respectively scalar and vector in nature.
For example, $\int_V \rho(\mathbf{r}) \,dV$ is the total mass of a fluid contained in a volume $V$ and $\int_V \rho(\mathbf{r}) \mathbf{v}(\mathbf{r}) \,dV$ is the total linear momentum of that.
References
- David Tong Vector Calculus Lecture Notes, 2024 - Chapter 1.2, 1.3, 2.2
- K.F. Riley Mathematical Methods for Physicists and Engineers, 1998 - Chapter 11.1, 11.4, 11.5, 11.6