Orthogonal Curvilinear Coordinates
Many physical systems possess spherical symmetry or axial symmetry in which it is more natural to use a different choice of coordinates. Two most common non-Cartesian coordinate systems are spherical and cylindrical polars.
In general, we can describe a point $\mathbf{x}$ in $\mathbb{R}^3$ using some coordinates $u, v, w$ so that $\mathbf{x} = (u, v, w)$. By partial differentiation, $\partial_u \mathbf{x}$, $\partial_v \mathbf{x}$ and $\partial_w \mathbf{x}$ are the tangent vectors to the lines defined by keeping the other two variables constants respectively.
Definition. The coordinate $(u, v, w)$ are orthogonal curvilinear if the three tangent vectors are mutually orthogonal everywhere. The tangent vectors can be normalized by writing
\[{\partial \mathbf{x} \over \partial u} = h_u \mathbf{e}_u, \qquad {\partial \mathbf{x} \over \partial v} = h_v \mathbf{e}_v, \qquad {\partial \mathbf{x} \over \partial w} = h_w \mathbf{e}_w\]with scale factors $h_u, h_v, h_w > 0$ and $\mathbf{e}_u \times \mathbf{e}_v = \mathbf{e}_w$ and $\mathbf{e}_i \cdot \mathbf{e}_j = \delta_{ij}$.
It is important that the basis vectors $\mathbf{e}_u, \mathbf{e}_v, \mathbf{e}_w$ above are specific to a point in space and are not constant. Therefore, the vector identities derived in Cartesian coordiantes might not apply in general, e.g. $\mathbf{a} \cdot \mathbf{b} \not= a_u b_u + a_v b_v + a_w b_w$.
Proposition. The Jacobian of the coordinate transformation is positive.
Proof.
Let $\mathbf{x} = (x_1(u_1, u_2, u_3), x_2(u_1, u_2, u_3), x_3(u_1, u_2, u_3))$,
\[\begin{align*} J &= \varepsilon_{ijk} {\partial x_i \over \partial u_i} {\partial x_j \over \partial u_j} {\partial x_k \over \partial u_k} \\ &= \varepsilon_{ijk} h_1 (\mathbf{e}_1)_i h_2 (\mathbf{e}_1)_j h_3 (\mathbf{e}_1)_k \\ &= h_1h_2h_3 (\mathbf{e}_1 \times (\mathbf{e}_2 \times \mathbf{e}_3)) \\ &= h_1h_2h_3 \\ \end{align*}\]
Proposition. The scale factors are the change in length as we change each of the coordinates.
Proof.
An infinitesimal vector displacement at position $\mathbf{x}$ is
\[d\mathbf{x} = h_u \mathbf{e}_u \,du + h_v \mathbf{e}_v \,dv + h_w \mathbf{e}_w \,dw\]Therefore, by squaring this, we have
\[(ds)^2 = (d\mathbf{x})^2 = d\mathbf{x} \cdot d\mathbf{x} = h_u^2 \,du^2 + h_v^2 \,dv^2 + h_w^2 \,dw^2\]
Definition. For curvilinear coordinates, the gradient $\nabla f$ is defined to be the vector such that for all $d\mathbf{x}$
\[df = \nabla f \cdot d\mathbf{x}\]which is a coordinate free definition.
Proposition. The gradient $\nabla f$ is given by
\[\nabla f = \sum_i {1 \over h_i} {\partial f \over \partial u_i} \mathbf{e}_i = \left( {1 \over h_u} {\partial f \over \partial u_u}, {1 \over h_v} {\partial f \over \partial u_v}, {1 \over h_w} {\partial f \over \partial u_w} \right)\]Proof.
Let $\nabla f = \sum_i \alpha_i \mathbf{e}_i$, then
\[df = \sum_i \alpha_i \mathbf{e}_i \cdot \sum_j h_j \mathbf{e}_j \,du_j = \sum_i \alpha_i h_i \,du_i\]By definition of differential, $df$ is given by
\[df = \sum_i {\partial f \over \partial u_i} \,du_i\]Hence,
\[\alpha_i = {1 \over h_i} {\partial f \over \partial u_i}\]
Proposition. The divergence $\nabla \cdot \mathbf{F}$ of a vector field $\mathbf{F}(u, v, w)$ is given by
\[\nabla \cdot \mathbf{F} = {1 \over h_uh_vh_w} \left( {\partial \over \partial u}(h_vh_wF_u) + {\partial \over \partial v}(h_uh_wF_v) + {\partial \over \partial w}(h_uh_vF_w) \right)\]
Proposition. The curl $\nabla \times \mathbf{F}$ of a vector field $\mathbf{F}(u, v, w)$ is given by
\[\nabla \times \mathbf{F} = {1 \over h_uh_vh_w} \begin{vmatrix} h_u \mathbf{e}_u & h_v \mathbf{e}_v & h_w \mathbf{e}_w \\ {\partial \over \partial u} & {\partial \over \partial v} & {\partial \over \partial w} \\ h_u F_u & h_v F_v & h_w F_w \end{vmatrix}\]
Proposition. The Laplacian $\nabla^2 f$ is given by
\[\nabla^2 f = {1 \over h_uh_vh_w} \left[ {\partial \over \partial u} \left( {h_vh_w \over h_u} {\partial f \over \partial u} \right) + {\partial \over \partial v} \left( {h_uh_w \over h_v} {\partial f \over \partial v} \right) + {\partial \over \partial w} \left( {h_uh_v \over h_w} {\partial f \over \partial w} \right) \right]\]
Proposition. The volume of an infinitesimal parallelepiped is given by
\[dV = h_uh_vh_w \,du\,dv\,dw\]Proof.
\[\begin{align*} dV &= \left| du {\partial \mathbf{x} \over \partial u} \cdot \left(dv {\partial \mathbf{x} \over \partial v} \times dw {\partial \mathbf{x} \over \partial w} \right) \right| \\ &= |du \,h_u \mathbf{e}_u \cdot (dv \,h_v \mathbf{e}_v \times dw \,h_w \mathbf{e}_w)| \\ &= h_uh_vh_w \,du\,dv\,dw \,|\mathbf{e}_u \cdot (\mathbf{e}_v \times \mathbf{e}_w)| \\ &= h_uh_vh_w \,du\,dv\,dw \end{align*}\]
Cartesian Coordinates
Obviously, $\mathbf{x} = (x, y, z)$ and hence $h_x = h_y = h_z = 1$ and $\mathbf{e}_x = \mathbf{i}$, $\mathbf{e}_y = \mathbf{j}$ and $\mathbf{e}_z = \mathbf{k}$. The expressions for gradient, divergence and curl can easily be verified to match those written in differential operators.
Cylindrical Polar Coordinates
Definition. The position of a point $P$ having Cartesian coordinates $(x, y, z)$ can be expressed as
\[x = \rho \cos \phi, \qquad y = \rho \sin \phi, \qquad z = z\]where $(\rho, \phi, z)$ is its cylindrical polar coordinates, with $\rho \ge 0$, $0 \le \phi < 2\pi$ and $z \in \mathbb{R}$. The inverses are
\[\rho = \sqrt{x^2, y^2} ,\qquad \phi = \tan^{-1} {y \over x} ,\qquad z = z\]
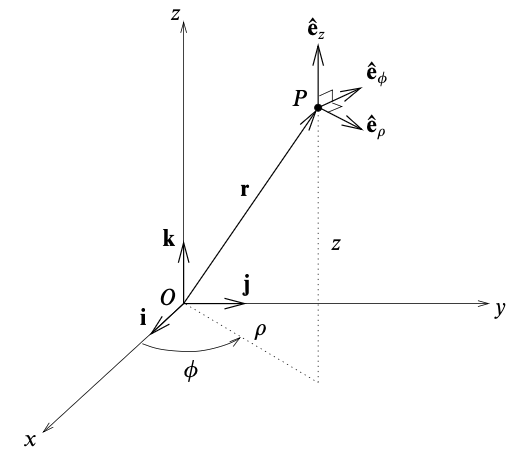
Proposition. The scale factors and unit vectors of cylindrical polars are
\[\begin{align*} h_\rho &= 1 \,,\quad &\mathbf{e}_\rho &= (\cos \phi, \sin \phi, 0) \\ h_\phi &= \rho \,,\quad &\mathbf{e}_\phi &= (-\sin \phi, \cos \phi, 0) \\ h_z &= 1 \,,\quad &\mathbf{e}_z &= (0, 0, 1) \end{align*}\]Proof.
The position vector of a point $P$ is $\mathbf{x} = (\rho \cos \phi, \rho \sin \phi, z)$. Thus,
\[\begin{align*} {\partial \mathbf{x} \over \partial \rho} &= (\cos \phi, \sin \phi, 0) \\ {\partial \mathbf{x} \over \partial \phi} &= (- \rho \sin \phi, \rho \cos \phi, 0) \\ {\partial \mathbf{x} \over \partial z} &= (0, 0, 1) \end{align*}\]The scale factors and unit vectors can be derived from the above. Cylindrical polars are a right-handed orthogonal curvilinear coorindate system since it satisfies $\mathbf{e}_i \cdot \mathbf{e}_j = \delta_{ij}$ and $\varepsilon_{ijk} \mathbf{e}_i = \mathbf{e}_j \times \mathbf{e}_k$.
Proposition. The Cartesian basis vectors in terms of cylindrical basis vectors of a point $\mathbf{x}(\rho, \phi, z)$ are
\[\begin{align*} \mathbf{i} &= \cos \phi \,\mathbf{e}_\rho - \sin \phi \,\mathbf{e}_\phi \\ \mathbf{j} &= \sin \phi \,\mathbf{e}_\rho + \cos \phi \,\mathbf{e}_\phi \\ \mathbf{k} &= \mathbf{e}_z \end{align*}\]Proof.
By finding the inverse of the coefficient matrix of the cylindrical basis vectors.
Proposition. The position vector $\mathbf{x}$ in cylindrical polars of a point is given by
\[\mathbf{x} = \rho \mathbf{e}_\rho + z \mathbf{e}_z\]Proof.
From the above, we can see that
\[\mathbf{x} = (\rho\cos\phi, \rho\sin\phi, z) = \rho (\cos\phi, \sin\phi, 0) + z (0, 0, 1) = \rho \mathbf{e}_\rho + z \mathbf{e}_z\]
Proposition. An infinitesimal vector displacement $d\mathbf{x}$ is given by
\[d\mathbf{x} = d\rho \,\mathbf{e}_\rho + \rho \,d\phi \,\mathbf{e}_\phi + dz \,\mathbf{e}_z\]and its magitude $ds$ is
\[(ds)^2 = (d\rho)^2 + \rho^2 (d\phi)^2 + (dz)^2\]
Proposition. The gradient is given by
\[\nabla f = {\partial f \over \partial \rho} \mathbf{e}_\rho + {1 \over \rho} {\partial f \over \partial \phi} \mathbf{e}_\phi + {\partial f \over \partial z} \mathbf{e}_z\]
Proposition. The divergence of a vector field $\mathbf{F}(\rho, \phi, z)$ is given by
\[\nabla \cdot \mathbf{F} = {1 \over \rho} {\partial (\rho F_\rho) \over \partial \rho} + {1 \over \rho} {\partial F_\phi \over \partial \phi} + {\partial F_z \over \partial z}\]
Proposition. The curl of a vector field $\mathbf{F}(\rho, \phi, z)$ is given by
\[\nabla \times \mathbf{F} = \left({1 \over \rho} {\partial F_z \over \partial \phi} - {\partial F_\phi \over \partial z} \right) \,\mathbf{e}_\rho + \left({\partial F_\rho \over \partial z} - {\partial F_z \over \partial \rho} \right) \,\mathbf{e}_\phi + {1 \over \rho} \left({\partial (\rho F_\phi) \over \partial \rho} - {\partial F_\rho \over \partial \phi} \right) \,\mathbf{e}_z\]
Proposition. The Laplacian is given by
\[\nabla^2 f = {1 \over \rho} {\partial \over \partial \rho} \left( \rho {\partial f \over \partial \rho} \right) + {1 \over \rho^2} {\partial^2 f \over \partial \phi^2} + {\partial^2 f \over \partial z^2}\]
Proposition. The volume of the infinitesimal parallelepiped is
\[dV = \rho \,d\rho \,d\phi \,dz\]
Spherical Polar Coordinates
Definition. The position of a point $P$ having Cartesian coordinates $(x, y, z)$ can be expressed as
\[x = r \sin \theta \cos \phi, \qquad y = r \sin \theta \sin \phi, \qquad z = r \cos \theta\]where $(r, \theta, \phi)$ is its spherical polar coordinates, with $r \ge 0$, $0 \le \theta \le \pi$ and $0 \le \phi < 2\pi$. The inverses are
\[r = \sqrt{x^2 + y^2 + z^2}, \qquad \theta = \tan^{-1} {\sqrt{x^2 + y^2} \over z}, \qquad \phi = \tan^{-1} {y \over x}\]
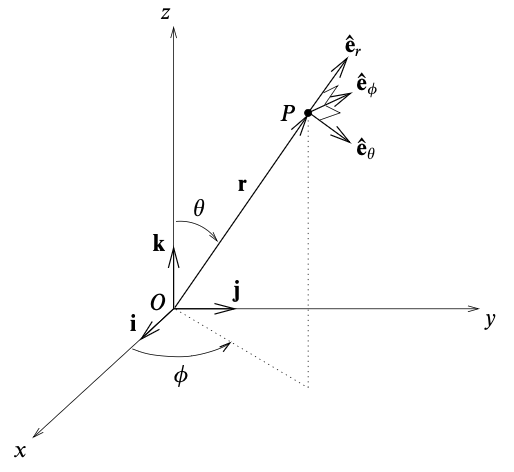
Proposition. The scale factors and unit vectors of spherical polars are
\[\begin{align*} h_r &= 1 \,,\quad &\mathbf{e}_r &= (\sin \theta \cos \phi, \sin \theta \sin \phi, \cos \theta) \\ h_\theta &= r \,,\quad &\mathbf{e}_\theta &= (\cos \theta \cos \phi, \cos \theta \sin \phi, - \sin \theta) \\ h_\phi &= r\sin\theta \,,\quad &\mathbf{e}_\phi &= (- \sin \phi, \cos \phi, 0) \end{align*}\]Proof.
The position vector of a point $P$ is $\mathbf{x} = (r \sin \theta \cos \phi, r \sin \theta \sin \phi, r \cos \theta)$. Thus,
\[\begin{align*} {\partial \mathbf{x} \over \partial r} &= (\sin \theta \cos \phi, \sin \theta \sin \phi, \cos \theta) \\ {\partial \mathbf{x} \over \partial \theta} &= (r \cos \theta \cos \phi, r \cos \theta \sin \phi, - r \sin \theta) \\ {\partial \mathbf{x} \over \partial \phi} &= (-r \sin \theta \sin \phi, r \sin \theta \cos \phi, 0) \end{align*}\]The scale factors and unit vectors can be derived from the above. Cylindrical polars are a right-handed orthogonal curvilinear coorindate system since it satisfies $\mathbf{e}_i \cdot \mathbf{e}_j = \delta_{ij}$ and $\varepsilon_{ijk} \mathbf{e}_i = \mathbf{e}_j \times \mathbf{e}_k$.
Proposition. The Cartesian basis vectors in terms of spherical basis vectors of a point $\mathbf{x}(r, \theta, \phi)$ are
\[\begin{align*} \mathbf{i} &= \sin \theta \cos \phi \,\mathbf{e}_r + \cos \theta \cos \phi \,\mathbf{e}_\theta - \sin\phi \,\mathbf{e}_\phi \\ \mathbf{j} &= \sin \theta \sin \phi \,\mathbf{e}_r + \cos \theta \sin \phi \,\mathbf{e}_\theta + \cos\phi \,\mathbf{e}_\phi \\ \mathbf{k} &= \cos \theta \,\mathbf{e}_r - \sin \theta \,\mathbf{e}_\theta \end{align*}\]Proof.
By finding the inverse of the coefficient matrix of the spherical basis vectors.
Proposition. The position vector $\mathbf{x}$ in spherical polars of a point is given by
\[\mathbf{x} = r \mathbf{e}_r\]Proof.
From the above, we can see that
\[\mathbf{x} = (r\sin\theta\cos\phi, r\sin\theta\sin\phi, r\cos\theta) = r (\sin\theta\cos\phi, \sin\theta\sin\phi, \cos\theta) = r \mathbf{e}_r\]
Proposition. An infinitesimal vector displacement $d\mathbf{x}$ is given by
\[d\mathbf{x} = dr \,\mathbf{e}_r + r \,d\theta \,\mathbf{e}_\theta + r \sin \theta \,d\phi \,\mathbf{e}_\phi\]and its magitude $ds$ is
\[(ds)^2 = (dr)^2 + r^2 (d\theta)^2 + r^2 \sin^2 \theta (d\phi)^2\]
Proposition. The gradient is given by
\[\nabla = \mathbf{e}_r {\partial \over \partial r} + \mathbf{e}_\theta {1 \over r} {\partial \over \partial \theta} + \mathbf{e}_\phi {1 \over r\sin\theta} {\partial \over \partial \phi}\]
Proposition. The divergence of a vector field $\mathbf{F}(\rho, \phi, z)$ is given by
\[\nabla \cdot \mathbf{F} = {1 \over r^2} {\partial (r^2 F_r) \over \partial r} + {1 \over r\sin \theta} {\partial (\sin \theta F_\theta) \over \partial \theta} + {1 \over r\sin \theta} {\partial F_\phi \over \partial \phi}\]
Proposition. The curl of a vector field $\mathbf{F}(\rho, \phi, z)$ is given by
\[\nabla \times \mathbf{F} = {1 \over r\sin\theta} \left( {\partial (\sin\theta F_\phi) \over \partial \theta} - {\partial F_\theta \over \partial \phi} \right) \,\mathbf{e}_r + {1 \over r} \left( {1 \over \sin\theta} {\partial F_r \over \partial \phi} - {\partial (r F_\phi) \over \partial r} \right) \,\mathbf{e}_\phi + {1 \over r} \left( {\partial (r F_\theta) \over \partial r} - {\partial F_r \over \partial \theta} \right) \,\mathbf{e}_\phi\]
Proposition. The Laplacian is given by
\[\nabla^2 f = {1 \over r^2} {\partial \over \partial r} \left( r^2 {\partial f \over \partial r} \right) + {1 \over r^2 \sin \theta} {\partial \over \partial \theta} \left( \sin \theta {\partial f \over \partial \theta} \right) + {1 \over r^2 \sin^2 \theta} {\partial^2 f \over \partial \phi^2}\]
Proposition. The volume of the infinitesimal parallelepiped is
\[dV = r^2 \sin \theta \,dr \,d\theta \,d\phi\]
References
- David Tong Vector Calculus Lecture Notes, 2024 - Chapter 2.1.4
- Stephen J. Cowley Vector Calculus Lectures Notes, 2000 - Chapter 7
- K.F. Riley Mathematical Methods for Physicists and Engineers, 1998 - Chapter 6.4, 10.9