Linear Maps
The crucial property of vectors spaces is that the linear combination of vectors are again a vector. The defining property of linear maps is that it preserves the linear combination in a natural way, i.e. image of a linear combination is a linear combination of the images, or $\mathcal{T}(\lambda x + \mu y) = \lambda \mathcal{T}(x) + \mu \mathcal{T}(y)$.
Definition. Let $V, W$ be vector spaces over a field $\mathbb{F}$. The map $\mathcal{T}: V \to W$ is a linear map or linear transformation if for all $a, b \in V$ and $\lambda, \mu \in \mathbb{F}$,
\[\begin{align*} \mathcal{T}(a + b) &= \mathcal{T}(a) + \mathcal{T}(b) \\ \mathcal{T}(\lambda a) &= \lambda \mathcal{T}(a) \end{align*}\]or equivalently
\[\mathcal{T}(\lambda a + \mu b) = \lambda \mathcal{T}(a) + \mu \mathcal{T}(b)\]
Lemma. $\mathcal{T}(0_V) = 0_W$.
Proof.
When $\lambda = \mu = 0$, we have
\[\mathcal{T}(0_V) = \mathcal{T}(0 a + 0 b) = 0 \mathcal{T}(a) + 0 \mathcal{T}(b) = 0_W\]
Image and Rank, Kernel and Nullity
Let $\mathcal{T}: V \to W$ be a linear map.
Definition. $\text{im}(\mathcal{T}) = \mathcal{T}(V)$ is the image of $V$ under $\mathcal{T}$.
Theorem. $\mathcal{T}(V)$ is a subspace of $W$.
Proof.
$0_W \in \mathcal{T}(V)$ so it is non-empty.
For all $\mathcal{T}(a), \mathcal{T}(b) \in \mathcal{T}(V)$, we have
\[\lambda \mathcal{T}(a) + \mu \mathcal{T}(b) = \mathcal{T}(\lambda a + \mu b) \in \mathcal{T}(V)\]
Definition. The rank of $\mathcal{T}$ is the dimension of the image, i.e.
\[r(\mathcal{T}) = \dim \mathcal{T}(V)\]
Definition. The kernel or nullspace of $\mathcal{T}$ is the subset of $V$ that maps to the zero element in $W$, i.e.
\[\ker \mathcal{T} = \Set{v \in V \mid \mathcal{T}(v) = 0_W}\]
Theorem. $\ker \mathcal{T}$ is a subspace of $V$.
$0_V \in \ker \mathcal{T}$ so it is non-empty.
For $a, b \in \ker \mathcal{T}$, we have
\[\mathcal{T}(\lambda a + \mu b) = \lambda \mathcal{T}(a) + \mu \mathcal{T}(b) = \lambda 0_W + \mu 0_W = 0_W\]Hence, $\lambda a + \mu b \in \ker \mathcal{T}$.
Definition. The nullity of $\mathcal{T}$ is the dimension of the kernel, i.e.
\[n(\mathcal{T}) = \dim \ker \mathcal{T}\]
Theorem. [Rank-Nullity Theorem] Let $\mathcal{T}: V \to W$ be a linear map, then
\[r(\mathcal{T}) + n(\mathcal{T}) = \dim V\]
Composition of Maps
Definition. Let $\mathcal{S}: U \to V$ and $\mathcal{T}: V \to W$ be linear maps such that
\[u \mapsto v = \mathcal{S}(u) \qquad v \mapsto w = \mathcal{T}(v)\]The composite map or product map $\mathcal{TS}$ is the map $\mathcal{TS}: U \to W$ such that
\[u \mapsto w = \mathcal{T}(\mathcal{S}(u))\]
For the map to be well defined, the domain of $\mathcal{T}$ must include the image of $\mathcal{S}$.
Bases and Matrix Representation
Let $\Set{\mathbf{e_j} \mid j = 1, …, n}, \Set{\mathbf{f_i} \mid i = 1, …, m}$ be the bases of vector spaces $V$ and $W$ respectively (not necessarily orthonormal). Any vector $\mathbf{x} \in V$ can be uniquely written as
\[\mathbf{x} = \sum_{j=1}^n x_j \mathbf{e}_j\]Let $\mathcal{A}: V \to W$, i.e. $\mathbf{x} \mapsto \mathbf{x}’ = \mathcal{A}(\mathbf{x})$ be a linear map. Because of the linearity of the map, we have
\[\mathbf{x}' = \mathcal{A}\left( \sum_{j=1}^n x_j \mathbf{e}_j \right) = \sum_{j=1}^n x_j \mathcal{A}(\mathbf{e}_j) = \sum_{j=1}^n x_j \mathbf{e}_j'\]By expressing $e_j’ \in W$ in components form, we have
\[\mathbf{e}_j' = \sum_{i=1}^m A_{ij} \mathbf{f}_i\]and therefore
\[\mathbf{x}' = \sum_{j=1}^n x_j \left( \sum_{i=1}^m A_{ij} \mathbf{f}_i \right) = \sum_{i=1}^m \left( \sum_{j=1}^n A_{ij} x_j \right) \mathbf{f}_i\]We can see that the $i$-th component of the image $\mathbf{x}’$ under $\mathcal{A}$ is
\[x_i' = A_{ij} x_j\]or alternatively in expanded form, we have
\[\begin{gather} x_1' = A_{11}x_1 + A_{12}x_2 + \dots + A_{1n}x_n \\ x_2' = A_{21}x_1 + A_{22}x_2 + \dots + A_{2n}x_n \\ \vdots \\ x_m' = A_{m1}x_1 + A_{m2}x_2 + \dots + A_{mn}x_n \end{gather}\]Base on the above, we conclude that linear maps can be represented by matrices, i.e.
Proposition. A linear map $\mathcal{A}: V \to W$ can be represented by the matrix
\[\mathsf{A} = \begin{pmatrix} A_{11} & A_{12} & \dots & A_{1n} \\ A_{21} & A_{22} & \dots & A_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ A_{m1} & A_{m2} & \dots & A_{mn} \\ \end{pmatrix}\]such that for colume matrices
\[\mathsf{x} = (x_1, x_2, ..., x_n) \qquad \mathsf{x}' = (x_1', x_2', ..., x_n')\]we have
\[\mathsf{x}' = \mathsf{A}\mathsf{x}\]We can also write
\[\mathsf{A} = \begin{pmatrix} \mathbf{e}_1' & \mathbf{e}_2' & ... & \mathbf{e}_n'\end{pmatrix}\]where $\mathbf{e}_j’ = \mathcal{A}(\mathbf{e}_j)$ is the column matrix of $\mathbf{e}_j$ with respect to $\Set{\mathbf{f}_i}$ after the transformation.
Recall that for a vector, the component form represents an actual coordinates only after we have specifed the basis. If we change the components, we get a different vector. If we change the basis, we get a different representation of the same vector.
The matrix $\mathsf{A}$ above is of the same nature, i.e. the component of the linear map $\mathcal{A}: V \to W$. It represents an actual “coordinates” of the map only if we have specified the bases, i.e. the bases of $V$ and $W$. If we change the components, we get a different map. If we change the bases, we get a different representation of the same map.
In other words, a linear map can have many matrix representations, but once the bases are chosen, we can find a unique matrix $\mathsf{A}$ as the components.
Examples
The following are some example maps $\mathbb{R}^3 \to \mathbb{R}^3$ with respect to typical orthonormal basis $\Set{\mathbf{e_j} \mid j = 1, 2, 3}$. To avoid ambiguity, we will use $\Set{\mathbf{f_i}} = \Set{\mathbf{e_j}}$ as the basis of the codomain.
Rotation
Proposition. The matrix for a rotation by an angle $\theta$ about the $x_3$ axis is
\[\mathsf{R}_\theta = \begin{pmatrix} \cos\theta & -\sin\theta & 0 \\ \sin\theta & \cos\theta & 0 \\ 0 & 0 & 1 \\ \end{pmatrix}\]Proof.
In order the find the matrix, we can find the image of the basis $\Set{\mathbf{e_j}}$ under the transformation, i.e.
\[\begin{align*} \mathbf{e_1} \mapsto \mathbf{e_1}' &= \mathbf{f_1} \cos\theta + \mathbf{f_2} \sin\theta \\ \mathbf{e_2} \mapsto \mathbf{e_2}' &= -\mathbf{f_1} \sin\theta + \mathbf{f_2} \cos\theta \\ \mathbf{e_3} \mapsto \mathbf{e_3}' &= \mathbf{f_3} \end{align*}\]
Proposition. The matrix for a rotation by an angle $\theta$ about a unit vector $\mathbf{\hat{n}} = (n_1, n_2, n_3)$ is
\[\mathsf{R}_{(\mathsf{\hat{n}}, \theta)} = \begin{pmatrix} n_1n_1(1 - \cos\theta) + \cos\theta & n_1n_2(1 - \cos\theta) - n_3\sin\theta & n_1n_3(1 - \cos\theta) + n_2\sin\theta \\ n_2n_1(1 - \cos\theta) + n_3\sin\theta & n_2n_2(1 - \cos\theta) + \cos\theta & n_2n_3(1 - \cos\theta) - n_1\sin\theta \\ n_3n_1(1 - \cos\theta) - n_2\sin\theta & n_3n_2(1 - \cos\theta) + n_1\sin\theta & n_3n_3(1 - \cos\theta) + \cos\theta \\ \end{pmatrix}\]or
\[\mathsf{R}_{ij} = \delta_{ij} \cos \theta + (1 - \cos\theta)n_in_j - \varepsilon_{ijk}n_k\sin\theta\]Proof.
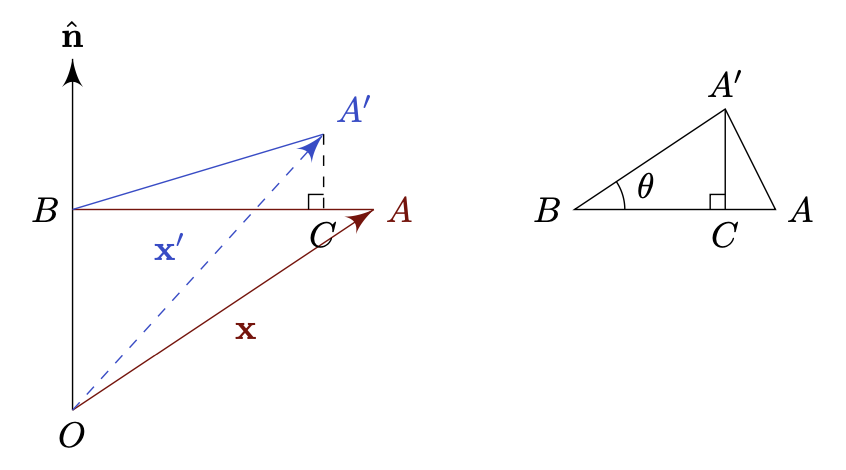
The image $\mathbf{x}’ = \vec{OB} + \vec{BC} + \vec{CA’}$.
We have
\[\begin{align*} \vec{OB} &= (\mathbf{x} \cdot \mathbf{\hat{n}}) \mathbf{\hat{n}} \\ \vec{BC} &= \vec{BA} \cos\theta \\ &= (\vec{BO} + \vec{OA}) \cos\theta \\ &= -\cos\theta(\mathbf{x} \cdot \mathbf{\hat{n}}) \mathbf{\hat{n}} + \cos\theta \mathbf{x} \\ \vec{CA'} &= \sin\theta (\hat{n} \times \mathbf{x}) \end{align*}\]Hence,
\[\mathbf{x}' = \cos\theta \mathbf{x} + (1 - \cos\theta)(\mathbf{x} \cdot \mathbf{\hat{n}}) \mathbf{\hat{n}} - \sin\theta (\mathbf{x} \times \mathbf{\hat{n}})\]With the above formula, we can derive the corresponding matrix $\mathsf{R} = \Set{R_{ij}}$ using suffix notation,
\[\begin{align*} (\mathbf{x}')_i &= x_i \cos\theta + (1 - \cos\theta)(x_jn_j)n_i - \varepsilon_{ijk} x_jn_k \sin\theta \\ R_{ij}x_j &= (\delta_{ij} \cos\theta + n_in_j(1 - \cos\theta) - \varepsilon_{ijk} n_k \sin\theta) x_j \\ \end{align*}\]Therefore, we have
\[R_{ij} = \delta_{ij} \cos\theta + n_in_j(1 - \cos\theta) - \varepsilon_{ijk} n_k \sin\theta \\\]
Reflection
Proposition. The matrix of a reflection $\mathcal{H}_\Pi$ in the plane $\Pi = \Set{\mathbf{x} \in \mathbb{R}^3 \mid \mathbf{x} \cdot \mathbf{n} = 0, |\mathbf{n}| = 1}$ is
\[\mathsf{H} = \begin{pmatrix} 1 - 2n_1^2 & -2n_1n_2 & -2n_1n_3 \\ -2n_2n_1 & 1-2n_2^2 & -2n_2n_3 \\ -2n_3n_1 & -2n_3n_2 & 1-2n_3^2 \\ \end{pmatrix}\]or
\[\mathsf{H}_{ij} = \delta_{ij} - 2 n_i n_j\]Proof.
For a point $P$, let $N$ be the foot of the perpendicular from $P$ to the plane, then $\vec{NP} = (\mathbf{x} \cdot \mathbf{n}) \mathbf{n}$.
The image $\vec{OP’} = \vec{OP} - 2 \vec{NP}$ and hence
\[\mathbf{x}' = \mathcal{H}_\Pi(\mathbf{x}) = \mathbf{x} - 2 (\mathbf{x} \cdot \mathbf{n}) \mathbf{n}\]
Dilatation
Definition. Dilatation is the effect of stretching or contracting a unit cube to a cuboid by different factors along different axes. Hence
\[\mathsf{D} = \begin{pmatrix} \lambda & 0 & 0 \\ 0 & \mu & 0 \\ 0 & 0 & \nu \end{pmatrix}\]If $\lambda = \mu = \nu$, the transformation is called a pure dilatation.
Shear
Definition. A simple shear is a transformation in the plane (e.g. $x_1x_2$-plane) that displaces points in one direction (e.g. $x_1$ direction) by an amount proportional to the distance in that plane from an axis (e.g. $x_1$-axis).
For example, $\mathcal{S}_\lambda$ is the transformation such that
\[\begin{align*} \mathbf{e_1} \mapsto \mathbf{e_1}' &= \mathbf{f_1} \\ \mathbf{e_2} \mapsto \mathbf{e_2}' &= \mathbf{f_2} + \lambda\mathbf{f_1} \\ \mathbf{e_3} \mapsto \mathbf{e_3}' &= \mathbf{f_3} \\ \end{align*}\]which displaces points in $x_1$ direction by $\lambda$ times distance from $x_1$-axis.
Hence, for the above shear transformation,
\[\mathsf{S}_\lambda = \begin{pmatrix} 1 & \lambda & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \\ \end{pmatrix}\]