Vectors
The discussion here focuses on vectors in 2D and 3D spaces, i.e. $\mathbb{R}^2$ and $\mathbb{R}^3$. It begins from defining vectors and various operations of them geometrically. It then can be extended to algebraic definitions and generalized to the concept of vector spaces.
Definition. In $\mathbb{R}^2$ and $\mathbb{R}^3$, a vector is a quantity that is specified by a (positive) magnitude and a direction in space.
A vector $\mathbf{v}$ is represented geometrically as a line segment $\vec{AB}$ with magnitude $|\mathbf{v}|$ and with direction from $A$ to $B$. With a chosen origin $O$, every point $P$ in 2D/3D space has a position vector $\mathbf{x} = \vec{OP}$.
Definition. A zero/null vector, denoted by $\mathbf{0}$, is a vector with zero magnitude, i.e. $|\mathbf{0}| = 0$.
Definition. Given a vector $\mathbf{v} \not = \mathbf{0}$, a unit vector that is in the same direction as $\mathbf{v}$ and magnitude equals to $1$, i.e.
\[\mathbf{\hat{v}} = {\mathbf{v} \over |\mathbf{v}|}\]
Vector Addition
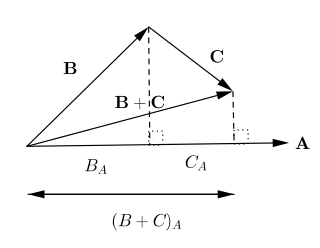
Definition. Vectors add according to the Parallelogram Law of Addition, i.e.
\[\mathbf{a} + \mathbf{b} = \mathbf{c} \iff \vec{OA} + \vec{OB} = \vec{OC}\]where $OACB$ is a parallelogram.
Property. Vector addition is/has
\[\mathbf{a} + \mathbf{b} = \mathbf{b} + \mathbf{a}\]
- [Commutative]
\[\mathbf{a} + (\mathbf{b} + \mathbf{c}) = (\mathbf{a} + \mathbf{b}) + c\]
- [Associative]
\[\mathbf{a} + \mathbf{0} = \mathbf{0} + \mathbf{a} = \mathbf{a}\]
- [Identity] The null/zero vector $\mathbf{0}$ is the additive identity, i.e.
\[\mathbf{a} + (-\mathbf{a}) = (-\mathbf{a}) + \mathbf{a} = \mathbf{0}\]
- [Inverse] The inverse of $\mathbf{a}$, namely $-\mathbf{a}$, is a vector parallel to $\mathbf{a}$ with same magitude, i.e. $|-\mathbf{a}| = |\mathbf{a}|$, but opposite direction, i.e.
Proof.
As $\vec{OA} = \vec{BC}$ and $\vec{OB} = \vec{AC}$ (opposite sides of the parallelogram), we have
\[\vec{OC} = \vec{OA} + \vec{AC} = \vec{OB} + \vec{BC}\]Hence, vector addition is commutative.
Other properties are geometrically self-evident.
Definition. Vector subtraction is the addition of inverse, i.e.
\[\mathbf{b} - \mathbf{a} = \mathbf{b} + (-\mathbf{a})\]
According to the above, the set of $\mathbb{R}^2$ / $\mathbb{R}^3$ vectors form a abelian group under addition.
Multiplication by Scalars
Definition. Let $\mathbf{a}$ be an vector and $\lambda \in \mathbb{R}$, $\lambda\mathbf{a}$ is defined as a vector parallel to $\mathbf{a}$, with magnitude $|\lambda| |\mathbf{a}|$ and same direction as $\mathbf{a}$ when $\lambda > 0$ and opposite direction to $\mathbf{a}$ when $\lambda < 0$.
Property. Multiplication by scalars is/has
\[\begin{align*} (\lambda + \mu)\mathbf{a} &= \lambda\mathbf{a} + \mu\mathbf{a} \\ \lambda (\mathbf{a} + \mathbf{b}) &= \lambda\mathbf{a} + \lambda\mathbf{b} \end{align*}\]
- [Distributive over vector addition]
\[\lambda(\mu\mathbf{a}) = (\lambda\mu)\mathbf{a}\]
- [Associative]
\[1\mathbf{a} = \mathbf{a}\]
- [Identity] $1 \in \mathbb{R}$ is the multiplicative identity, i.e.
Proposition. $0\mathbf{a} = \mathbf{0}$ and $(-1)\mathbf{a} = -\mathbf{a}$.
Linear Combination
Definition. The vector $\mathbf{c} = \lambda \mathbf{a} + \mu \mathbf{b}$ is a linear combination of $\mathbf{a}$ and $\mathbf{b}$.
Scalar Product
Definition. The scalar/dot product of two vectors $\mathbf{a}$ and $\mathbf{b}$ is defined to be the scalar number
\[\mathbf{a} \cdot \mathbf{b} = |\mathbf{a}| |\mathbf{b}|\cos\theta\]where $0 \le \theta \le \pi$ is the non-reflex angle between $\mathbf{a}$ and $\mathbf{b}$ once they are placed “tail to tail” or “head to head”.
Property. Scalar multiplication is commutative, i.e.
\[\mathbf{a} \cdot \mathbf{b} = \mathbf{b} \cdot \mathbf{a}\]
Property. A scalar product of a vector with itself is always $\ge 0$, i.e.
\[\mathbf{a} \cdot \mathbf{a} = |\mathbf{a}|^2 \ge 0\]with equality holds iff $\mathbf{a} = \mathbf{0}$.
Proposition. The “binomial expansion” of vectors is
\[(\mathbf{a} - \mathbf{b})^2 = \mathbf{a} \cdot \mathbf{a} + \mathbf{b} \cdot \mathbf{b} - 2(\mathbf{a} \cdot \mathbf{b})\]Proof.
Consider a triangle in 2D with $O, A, B$ as the vertices and $\theta = \angle BOA$. By Cosine Law, we have
\[|BA|^2 = |OA|^2 + |OB|^2 - 2|OA||OB|\cos\theta\]Let $\mathbf{a} = \vec{OA}$ and $\mathbf{b} = \vec{OB}$, we have $\vec{BA} = \mathbf{a} - \mathbf{b}$, we have
\[|\mathbf{a} - \mathbf{b}|^2 = |\mathbf{a}|^2 + |\mathbf{b}|^2 - 2|\mathbf{a}||\mathbf{b}|\cos\theta\]Hence, as $\mathbf{v} \cdot \mathbf{v} = \vert v \vert^2$,
\[(\mathbf{a} - \mathbf{b})^2 = (\mathbf{a} - \mathbf{b}) \cdot (\mathbf{a} - \mathbf{b}) = \mathbf{a} \cdot \mathbf{a} + \mathbf{b} \cdot \mathbf{b} - 2(\mathbf{a} \cdot \mathbf{b})\]
Proposition. If $\mathbf{a} \cdot \mathbf{b} = 0$ and $\mathbf{a} \not = \mathbf{0}$ and $\mathbf{b} \not = \mathbf{0}$, then $\mathbf{a} \perp \mathbf{b}$ and $\theta = \pi/2$.
Projection
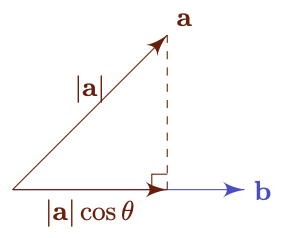
Definition. The projection of $\mathbf{a}$ onto $\mathbf{b}$ is the part of $\mathbf{a}$ that is parallel to $\mathbf{b}$, denoted by $\mathbf{a}^{\perp}$.
Theorem. $\mathbf{a}^{\perp} = (|\mathbf{a}|\cos\theta)\,\mathbf{\hat{b}} = (\mathbf{a} \cdot \mathbf{\hat{b}})\,\mathbf{\hat{b}}$.
Proof.
When $0 \le \theta \le \pi/2$, $|\mathbf{a}^{\perp}| = |\mathbf{a}| \cos \theta$ and $\mathbf{a}^{\perp}$ is in same direction as $\mathbf{b}$, i.e.
\[\mathbf{a}^{\perp} = (|\mathbf{a}|\cos\theta)\,\mathbf{\hat{b}}\]When $\pi / 2 < \theta \le \pi$, $|\mathbf{a}^{\perp}| = |\mathbf{a}| \cos (\pi - \theta)$ and $\mathbf{a}^{\perp}$ is in opposite direction as $\mathbf{b}$, i.e.
\[\mathbf{a}^{\perp} = \left(-|\mathbf{a}|\cos(\pi -\theta)\right)\,\mathbf{\hat{b}} = (|\mathbf{b}|\cos\theta)\,\mathbf{\hat{b}}\]Hence,
\[\mathbf{a}^{\perp} = |\mathbf{a}|{\mathbf{a} \cdot \mathbf{b} \over |\mathbf{a}||\mathbf{b}|}\mathbf{\hat{b}} = {\mathbf{a} \cdot \mathbf{b} \over |\mathbf{b}|^2}\mathbf{b} = (\mathbf{a} \cdot \mathbf{\hat{b}})\,\mathbf{\hat{b}}\]
Distributive over Addition
Lemma. For $\lambda \in \mathbb{R}$,
\[\mathbf{a} \cdot (\lambda \mathbf{b}) = (\lambda \mathbf{a}) \cdot \mathbf{b} = \lambda \mathbf{a} \cdot \mathbf{b}\]
Theorem. Scalar multiplication is distributive over vector addition, i.e.
\[\mathbf{a} \cdot (\mathbf{b} + \mathbf{c}) = \mathbf{a} \cdot \mathbf{b} + \mathbf{a} \cdot \mathbf{c}\]Proof.
According to the above, we can see that $\mathbf{b}^{\perp} + \mathbf{c}^{\perp} = (\mathbf{b} + \mathbf{c})^{\perp}$, i.e.
\[{\mathbf{a} \cdot \mathbf{b} \over |\mathbf{a}|^2}\mathbf{a} + {\mathbf{a} \cdot \mathbf{c} \over |\mathbf{a}|^2}\mathbf{a} = {\mathbf{a} \cdot (\mathbf{b} + \mathbf{c}) \over |\mathbf{a}|^2}\mathbf{a} \\\]By multiplying both side by $\vert \mathbf{a} \vert^2$ and taking dot product by $\mathbf{a}$,
\[(\mathbf{a} \cdot \mathbf{b} + \mathbf{a} \cdot \mathbf{c})(\mathbf{a} \cdot \mathbf{a}) = [\mathbf{a} \cdot (\mathbf{b} + \mathbf{c})](\mathbf{a} \cdot \mathbf{a}) \\\]Hence,
\[\mathbf{a} \cdot \mathbf{b} + \mathbf{a} \cdot \mathbf{c} = \mathbf{a} \cdot (\mathbf{b} + \mathbf{c})\]
In general,
\[\begin{align*} \mathbf{a} \cdot (\lambda \mathbf{b} + \mu \mathbf{c}) = \mathbf{a} \cdot (\lambda \mathbf{b}) + \mathbf{a} \cdot (\mu \mathbf{c}) = \lambda \mathbf{a} \cdot \mathbf{b} + \mu \mathbf{a} \cdot \mathbf{c} \end{align*}\]In vector space, this property is called linearity in the second argument. In fact, as scalar multiplication of vectors in real vector spaces is commutative, we also have linearity in the first argument (which might not be true in other vector spcaes).
Cauchy-Schwarz Inequality
Theorem. [Cauchy-Schwarz Inequality] For all $\mathbf{a}, \mathbf{b} \in \mathbb{R}^2$,
\[| \mathbf{a} \cdot \mathbf{b} | \le | \mathbf{a}| | \mathbf{b}|\]with equality holds when $\mathbf{a} = \mathbf{0}$ or $\mathbf{b} = \mathbf{0}$ or $\mathbf{a} = \lambda\mathbf{b}$.
Proof.
By definition,
\[|\mathbf{a} \cdot \mathbf{b}| = |\mathbf{a}||\mathbf{b}||\cos \theta| \le |\mathbf{a}||\mathbf{b}|\]as $\vert \cos \theta \vert \le 1$.
Proof that can be generalized to other vector spaces can be found here.
Triangle Inequality
Theorem. [Triangle Inequality]
\[\vert \mathbf{a} + \mathbf{b} \vert \le \vert \mathbf{a} \vert + \vert \mathbf{b} \vert\]
Corollary. $\vert \mathbf{a} - \mathbf{b} \vert \ge \vert \vert \mathbf{a} \vert - \vert \mathbf{b} \vert \vert$.
Vector Product
The vector product is only defined for $\mathbb{R}^3$ space but not all vector spaces in general.
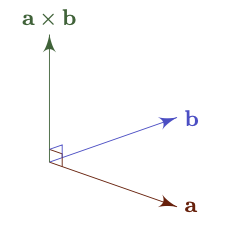
Definition. The vector/cross product $\mathbf{a} \times \mathbf{b}$ of an ordered pair $\mathbf{a}, \mathbf{b}$ is a vector such that
The magnitude of $\mathbf{a} \times \mathbf{b}$ is
\[\vert \mathbf{a} \times \mathbf{b} \vert = \vert \mathbf{a} \vert \vert \mathbf{b} \vert \sin \theta\]with $0 \le \theta \le \pi$ and definition similar to dot product (non-reflex angle after “tail-to-tail” or “head-to-head” placement of the two vectors).
$\mathbf{a} \times \mathbf{b}$ is orthongonal to both $\mathbf{a}$ and $\mathbf{b}$ (if $\mathbf{a} \times \mathbf{b} \not = \mathbf{0}$)
$\mathbf{a} \times \mathbf{b}$ has the direction defined by “right-hand rule” ($\mathbf{a}$ - index finger, $\mathbf{b}$ - second finger, $\mathbf{a} \times \mathbf{b}$ - thumb)
Property. ${1 \over 2} \mathbf{a} \times \mathbf{b}$ is the vector area of triangle $OAB$. $\mathbf{a} \times \mathbf{b}$ is the vector area of parallelogram $OACB$.
Proof.
For triangle $OAB$,
\[\text{Area of } OAB = {1 \over 2}|\mathbf{a}||\mathbf{b}| \sin \theta = {1 \over 2}|\mathbf{a} \times \mathbf{b}|\]For parallelogram $OACB$,
\[\text{Area of } OACB = \text{Area of } OAB \times 2 = |\mathbf{a} \times \mathbf{b}|\]The direction of $\mathbf{a} \times \mathbf{b}$ is orthogonal to the triangle/parallelogram.
Property. Vector product is anti-commutative, i.e.
\[\mathbf{a} \times \mathbf{b} = - \mathbf{b} \times \mathbf{a}\]
Property. Vector product of a vector with itself is a zero vector, i.e.
\[\mathbf{a} \times \mathbf{a} = \mathbf{0}\]
Property. Given $\mathbf{a} \not = \mathbf{0}$ and $\mathbf{b} \not = \mathbf{0}$
\[\mathbf{a} \times \mathbf{b} = \mathbf{0} \implies \mathbf{a} = \lambda \mathbf{b}\]i.e. $\mathbf{a}$ and $\mathbf{b}$ are parallel and $\theta = 0$ or $\theta = \pi$.
Distributive over Addition
Lemma. For $\lambda \in \mathbb{R}$,
\[\mathbf{a} \times (\lambda\mathbf{b}) = (\lambda \mathbf{a}) \times \mathbf{b} = \lambda ( \mathbf{a} \times \mathbf{b})\]
Theorem. Vector product is distributive over vector addition, i.e.
\[\mathbf{a} \times (\mathbf{b} + \mathbf{c}) = \mathbf{a} \times \mathbf{b} + \mathbf{a} \times \mathbf{c}\]Proof.
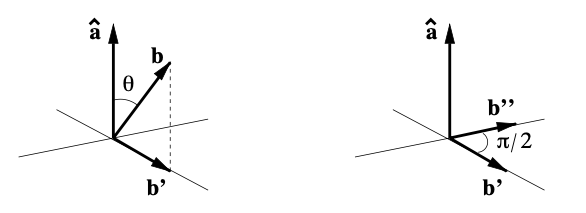
The vector product $\mathbf{\hat{a}} \times \mathbf{b}$ can be constructed by two steps. First project $\mathbf{b}$ onto a plane orthogonal to $\mathbf{\hat{a}}$ and then rotate the projection $\mathbf{b’}$ by $\pi/2$ in “anti-clockwise” direction (when looking in the opposite direction of $\mathbf{\hat{a}}$) to form $\mathbf{b’’}$.
We can see that $|\mathbf{b}’’| = |\mathbf{b’}| = |\mathbf{b}| \sin \theta$. By construction, $\mathbf{b’’} = \mathbf{\hat{a}} \times \mathbf{b}$.
Algebraically, with the properties of triple scaler product shown below, let $\mathbf{d} = \mathbf{a} \times (\mathbf{b} + \mathbf{c}) - \mathbf{a} \times \mathbf{b} - \mathbf{a} \times \mathbf{c}$,
\[\begin{align*} \mathbf{d} \cdot \mathbf{d} &= \mathbf{d} \cdot [\mathbf{a} \times (\mathbf{b} + \mathbf{c})] - \mathbf{d} \cdot (\mathbf{a} \times \mathbf{b}) - \mathbf{d} \cdot (\mathbf{a} \times \mathbf{c}) \\ &= (\mathbf{b} + \mathbf{c}) \cdot (\mathbf{d} \times \mathbf{a}) - \mathbf{b} \cdot (\mathbf{d} \times \mathbf{a}) - \mathbf{c} \cdot (\mathbf{d} \times \mathbf{a}) \\ &= 0 \end{align*}\]Hence, $\mathbf{d} = \mathbf{0}$ and $\mathbf{a} \times (\mathbf{b} + \mathbf{c}) = \mathbf{a} \times \mathbf{b} + \mathbf{a} \times \mathbf{c}$.
In general, similar to dot product,
\[\mathbf{a} \times (\lambda\mathbf{b} + \mu\mathbf{c}) = \lambda\mathbf{a} \times \mathbf{b} + \mu\mathbf{a} \times \mathbf{c}\]Scalar Triple Product
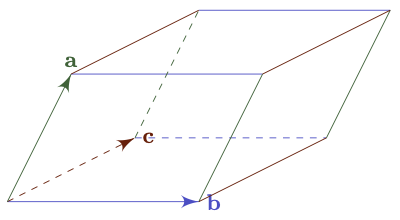
Definition. The scalar triple product is defined by
\[[\mathbf{a}, \mathbf{b}, \mathbf{c}] = \mathbf{a} \cdot(\mathbf{b} \times \mathbf{c})\]
Proposition. The scalar triple product represents the vector volume of parallelepiped.
Proof.
\[\begin{align*} \text{Volume} &= \text{Base Area} \times \text{Height} \\ &= |a||\mathbf{b} \times \mathbf{c}|cos\theta \\ &= \mathbf{a} \cdot(\mathbf{b} \times \mathbf{c}) \end{align*}\]
if $\mathbf{a}, \mathbf{b}, \mathbf{c}$ have the sense of the right-hand rule.
Proposition. If $\mathbf{a}, \mathbf{b}, \mathbf{c}$ have the sense of the right-hand rule, then
\[[\mathbf{a}, \mathbf{b}, \mathbf{c}] = [\mathbf{b}, \mathbf{c}, \mathbf{a}] = [\mathbf{c}, \mathbf{a}, \mathbf{b}] = -[\mathbf{b}, \mathbf{a}, \mathbf{c}] = - [\mathbf{a}, \mathbf{c}, \mathbf{b}] = - [\mathbf{c}, \mathbf{b}, \mathbf{a}]\]Proof.
The order of $\mathbf{a}, \mathbf{b}, \mathbf{c}$ doesn’t affect the volume of a parallelepiped given by $[\mathbf{a}, \mathbf{b}, \mathbf{c}]$.
$(\mathbf{b}, \mathbf{a}, \mathbf{c}), (\mathbf{a}, \mathbf{c}, \mathbf{b}), (\mathbf{c}, \mathbf{b}, \mathbf{a})$ have the sence of left-hand rule so it equals to the “negative volume”.
Proposition. $\mathbf{a} \cdot (\mathbf{b} \times \mathbf{c}) = (\mathbf{a} \times \mathbf{b}) \cdot \mathbf{c}$.
Proof.
From the above, $\mathbf{a} \cdot (\mathbf{b} \times \mathbf{c}) = \mathbf{c} \cdot (\mathbf{a} \times \mathbf{b})$ and dot product is commutative.
Theorem. Non-zero vectors $\mathbf{a}, \mathbf{b}, \mathbf{c}$ are coplanar iff $[\mathbf{a}, \mathbf{b}, \mathbf{c}] = 0$.
Proof.
$[\mathbf{a}, \mathbf{b}, \mathbf{c}] = 0 \iff$ The volume of the parallelepiped is zero $\iff \mathbf{a}, \mathbf{b}, \mathbf{c}$ are coplanar.
Vector Triple Product
Definition. The vector triple product is defined by
\[(\mathbf{a} \times \mathbf{b}) \times \mathbf{c} = - \mathbf{c} \times (\mathbf{a} \times \mathbf{b}) = - (\mathbf{b} \times \mathbf{a}) \times \mathbf{c} = \mathbf{c} \times (\mathbf{b} \times \mathbf{a})\]
Proposition. $\mathbf{a} \times (\mathbf{b} \times \mathbf{c}) = (\mathbf{a} \cdot \mathbf{c}) \mathbf{b} - (\mathbf{a} \cdot \mathbf{b}) \mathbf{c}$
Proof.
See Standard Basis and Suffix Notation.
We can see that the resulting vector has no component in direction $\mathbf{a}$ (outside the parentheses) because the resulting vector after the last vector multiplication by $\mathbf{a}$ is orthogonal to $\mathbf{a}$.
Vector Equations
We use vector manipulation on the equation so to simplify the terms, normally by dotting or crossing the equation with some vectors.
Problem. Solve $\mathbf{x} - (\mathbf{x} \times \mathbf{a}) \times \mathbf{b} = \mathbf{c}$.
Solution.
By dotting with $\mathbf{b}$ on both side, we have
\[\mathbf{x} \cdot \mathbf{b} = \mathbf{c} \cdot \mathbf{b}\]Also, by expanding $(\mathbf{x} \times \mathbf{a}) \times \mathbf{b}$, we have
\[(\mathbf{x} \times \mathbf{a}) \times \mathbf{b} = \mathbf{b} \times (\mathbf{a} \times \mathbf{x}) = (\mathbf{b} \cdot \mathbf{x})\mathbf{a} - (\mathbf{b} \cdot \mathbf{a})\mathbf{x}\]Hence,
\[\begin{align*} \mathbf{x} - (\mathbf{b} \cdot \mathbf{x})\mathbf{a} + (\mathbf{b} \cdot \mathbf{a})\mathbf{x} &= \mathbf{c} \\ (1 + (\mathbf{a} \cdot \mathbf{b}))\mathbf{x} &= \mathbf{c} + (\mathbf{b} \cdot \mathbf{c})\mathbf{a} \\ \mathbf{x} &= {\mathbf{c} + (\mathbf{b} \cdot \mathbf{c})\mathbf{a} \over 1 + \mathbf{a} \cdot \mathbf{b}} \end{align*}\]
Another technique can be found here.