Sequences
Definition. A sequence is a function $a: \mathbb{N} \to A$, denoted by $(a_n)$ or $(a_n)_1^\infty$ or $(a_n)_{n=1}^\infty$.
We want to study what it means for a real sequence to converge.
Definition. Let $(a_n)$ be a sequence and $L \in \mathbb{R}$. Then $(a_n)$ converges to $L$ or $a_n \to L$ if
\[(\forall \varepsilon > 0)(\exists N \in \mathbb{N})(\forall n \ge N)\;|a_n - L| < \varepsilon\]We then also write
\[\lim_{n \to \infty} a_n = L\]The sequence is said to be convergent, otherwise it is divergent.
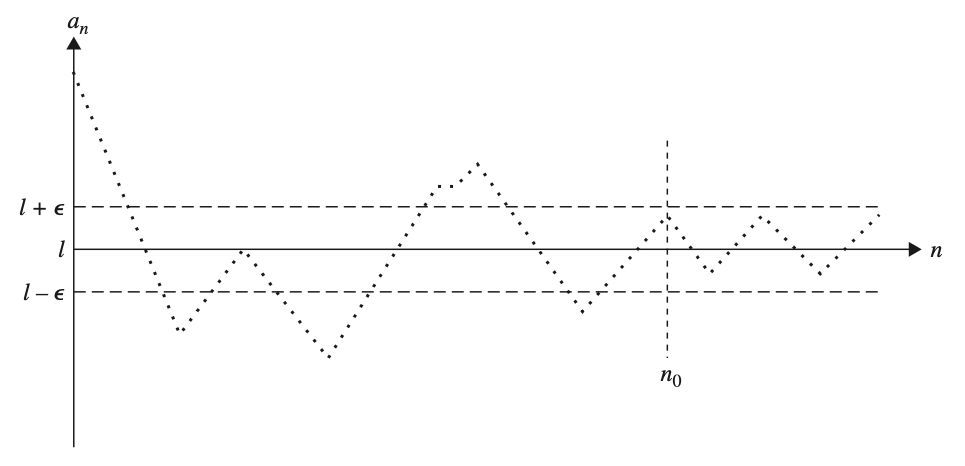
It is similar to the definition of limit of a function $f(x)$, therefore
\[\lim_{x \to \infty} f(x) = L \text{ and } f(n) = a_n \implies \lim_{n \to \infty} a_n = L\]Proposition. The limit is unique, i.e. if $a_n \to L_1$ and $a_n \to L_2$ then $L_1 = L_2$.
Proof.
Let $\varepsilon = \vert L_1 - L_2 \vert / 3$. There exists $N_1$ and $N_2$ such that
\[(\forall n \ge N_1)\; |a_n - L_1| < \varepsilon \quad \text{and} \quad (\forall n \ge N_2)\; |a_n - L_2| < \varepsilon\]Hence, let $N = \max(N_1, N_2)$, we have
\[(\forall n > N) |L_1 - L_2| \le |a_n - L_1| + |a_n - L_2| < 2\varepsilon = 2|L_1 - L_2|/3\]which is a contradiction except for $L_1 = L_2$.
Definition. $(a_n)$ is a null sequence if
\[(\forall \varepsilon > 0)(\exists N \in \mathbb{N})(\forall n \ge N)\;|a_n| < \varepsilon\]
Lemma. $a_n \to a$ iff $(a_n - a)$ is a null sequence.
Bounded Sequences
Definition. A sequence is bounded above if
\[(\exists M)(\forall n)\;a_n \le M\]
Definition. A sequence is bounded below if
\[(\exists m)(\forall n)\;a_n \ge m\]
Definition. A sequence is bounded if it is bounded above and below, i.e.
\[(\exists M)(\forall n)\; |a_n| \le M\]Otherwise it is unbounded.
Definition. A sequence is eventually bounded if
\[(\exists M)(\exists N)(\forall n \ge N)\; |a_n| \le M\]
Lemma. Every eventually bounded sequence is bounded.
Proof.
Obviously, the eventually bounded sequence is bounded by $\max(\vert a_1 \vert, …, \vert a_{N-1} \vert, M)$.
It can be useful for proving sequence to be bounded by showing it is eventually bounded.
Lemma. Every convergent sequence is bounded.
Proof.
Let $\varepsilon = 1$, there exists $N$ such that for all $n > N$, $\vert a_{n} - L \vert < 1$ and hence $(a_{n})$ is eventually bounded by $L + 1$.
Divergent Sequences
There are two cases for a sequence to be divergent.
Definition. The sequence $a_n$ is said to diverge to $+\infty$ or tend to infinity if
\[(\forall A \in \mathbb{R})(\exists N \in \mathbb{N})(\forall n > N)\; a_n > A\]
Similarily,
\[a_n \to -\infty \implies (\forall A \in \mathbb{R})(\exists N \in \mathbb{N})(\forall n > N)\; a_n < A\]Definition. If the sequence $(a_n)$ does not tend to a limit or to $\pm \infty$, it is said to be oscillating. If $(a_n)$ oscillates and bounded, it oscillates finitely. If $(a_n)$ oscillates and is not bounded, it oscillates infinitely.
Sums and Products
Lemma. If $(a_n)$ and $(b_n)$ are null sequences, then $(a_n + b_n)$ is also a null sequence.
Proof.
For any $\varepsilon > 0$, there exists $N_1$ and $N_2$ such that
\[(\forall n > N_1)\; |a_n| < \varepsilon / 2 \quad \text{and} \quad (\forall n > N_2)\; |b_n| < \varepsilon / 2\]Let $N = \max(N_1, N_2)$, then by triangle inequality,
\[(\forall n > N)\; |(a_n + b_n)| \le |a_n| + |b_n| < \varepsilon\]
Theorem. [Sum of Sequences] If $a_n \to a$ and $b_n \to b$, then $a_n + b_n \to a + b$.
Proof.
\[(a_n + b_n) - (a + b) = (a_n - a) + (b_n - b)\]$(a_n - a)$ and $(b_n - b)$ are null sequences and hence $((a_n + b_n) - (a + b))$ is also a null sequence.
Lemma. If $(a_n)$ is a null sequence and $(b_n)$ is a bounded sequence, then $(a_nb_n)$ is a null sequence.
Proof.
Let $(b_n)$ be bounded by $M$. For any $\varepsilon > 0$, there exists $N$ such that
\[(\forall n > N)\; |a_n| < \varepsilon / M\]Therefore,
\[(\forall n > N)\; |a_nb_n| = |a_n||b_n| < (\varepsilon / M)(M) = \varepsilon\]
Corollary. If $(a_n)$ is a null sequence and $c$ is a constant, then $(ca_n)$ is a null sequence.
Theorem. [Product of Sequences] If $a_n \to a$ and $b_n \to b$, then $a_nb_n \to ab$.
Proof.
\[a_nb_n - ab = (a_n - a)b_n + a(b_n - b)\]$(a_n - a)$ is a null sequence and $(b_n)$ is bounded, therefore $(a_n - a)b_n$ is a null sequence.
$(b_n - b)$ is a null sequence and $a$ is a constant, therefore $a(b_n - b)$ is a null sequence.
Hence, $(a_nb_n - ab)$ is also a null sequence.
Lemma. If $a_n \to a$, where $a \not= 0$, then $1/a_n \to 1/a$.
Proof.
\[{1 \over a_n} - {1 \over a} = {a - a_n \over aa_n}\]We have to show that $1 / a_n$ is bounded, meaning we need to have $\vert a_n \vert$ be greater than something.
Consider
\[|a| = |a_n + (- a_n + a)| \le |a_n| + |a_n - a| \implies |a_n| \ge |a| - |a_n - a|\]Therefore, for $\varepsilon = \vert a \vert / 2$, there exists $N$ such that
\[(\forall n > N)\;\vert a_n - a \vert \le {|a| \over 2} \implies |a_n| \ge |a| - |a_n - a| \ge {|a| \over 2} \implies {1 \over |a_n|} \le {2 \over |a|}\]so $1 / a_n$ is bounded.
As $(a - a_n)$ is null sequence, $1/a$ is a constant and $(1 / a_n)$ is bounded, their product is a null sequence and hence $1 / a_n \to 1 / a$.
Theorem. [Quotient of Sequences] If $a_n \to a$ and $b_n \to b$, where $b \not= 0$, then $a_n / b_n \to a / b$.
Proof.
$a_n \to a$ and $1/b_n \to 1/b$ so their product $a_n/b_n \to a/b$.
Convergence Test
Working directly with an arbitrary $\varepsilon$ can be difficult. Sometimes it can be easier to relate the sequence with other known converging sequences so to prove convergence and find the limit.
Proposition. [Sandwich Principle/Squeeze Theorem] Suppose that $a_n \le b_n \le c_n$ for all $n$. If $a_n \to L$ and $c_n \to L$, then $b_n \to L$.
Proof.
Given $\varepsilon > 0$, there exists an $N$ such that $\vert a_n - L \vert < \varepsilon$ and $\vert a_n - L \vert < \varepsilon$ for $n \ge N$, therefore
\[L - \varepsilon < a_n \le b_n \le c_n < L + \varepsilon\]
Corollary. $(a_n)$ is a null sequence if $(\vert a_n \vert)$ is a null sequence.
Proof.
\[-|a_n| \le a_n \le |a_n| \quad \text{and} \quad |a_n| \to 0 \implies -|a_n| \to 0\]By Sandwich Principle, $a_n \to 0$.
It is useful for finding limits of alternating sequence, for example
\[\lim_{n \to \infty} \left| {(-1)^n \over n} \right| = 0 \implies \lim_{n \to \infty} {(-1)^n \over n} = 0\]Proposition. Suppose that $(\varepsilon_k)$ is a null sequence of positive numbers. Then a sequence $(a_n)$ converges to $L$ iff for each $k$ there exists $N_k$ such that $\vert a_n - L \vert < \varepsilon_k$ for $n > N_k$.
Proof.
($\Rightarrow$) Certainly, given $\varepsilon = \varepsilon_k$, there exists $N = N_k$ such that $\vert a_n - L \vert < \varepsilon_k$ for $n > N_k$.
($\Leftarrow$) Given $\varepsilon > 0$, there exists a $k$ such that $0 < \varepsilon_k < \varepsilon$. For $n > N_k$, we have $\vert a_n - L \vert < \varepsilon_k < \varepsilon$.
It relates the sequence with a null sequence. We can prove convergence by showing for a term $\varepsilon_k$ in a shrinking distance, there is a point $N_k$ in the sequence such that the distance of points are within $\varepsilon_k$ from the limit. Convenient choices are $\varepsilon_k = 1/k$ or $\varepsilon_k = 1/2^k$.
The following test involves some knowledge about series.
Proposition. [Ratio Test] If
\[\lim_{n \to \infty} \left| { a_{n+1} \over a_n} \right| < 1\]then $(a_n)$ is a null sequence.
Proof.
By d’Alembert’s ratio test, the series $\sum a_n$ converges. Hence, the underlying sequence $(a_n)$ must be a null sequence.
Recurrence Relation
A sequence can be determined by a relation between successive members of it. For example, the famous Fibonacci sequence
\[a_{n+2} = a_{n+1} + a_n\]Sometimes, it is possible to find an explicit formula (See Difference Equations) but most of the time it is not possible. We can still study its limit by the following technique.
Proposition. If $a_n \to L$, then $a_{n+1} \to L$ and $a_{n+2} \to L$ and …
For example, if the sequence
\[a_{n+1} = \sqrt{a_n + a}\]has a limit $L$, then $L = \sqrt{L + a}$.
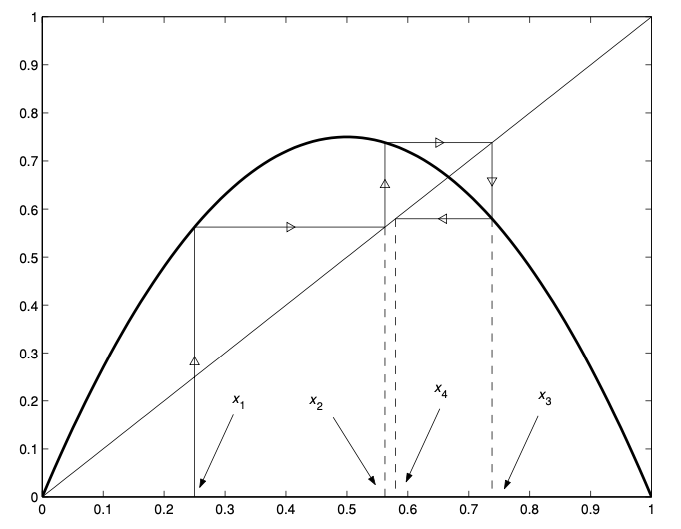
In some cases, the cobweb diagram can be useful as well.
References
- J C Burkill A First Cource in Mathematical Analysis, 1978 - Chapter 2
- D. J. H. Garling A Course in Mathematical Analysis Vol.1, 2013 - Chapter 3