Multiple Integrals
Just as we may consider derivatives with respect to multiple variables, we can do the same for integrals.
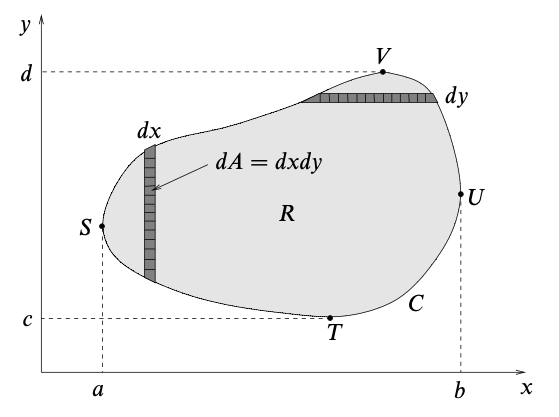
Definition. Suppose that $f(x, y)$ is a function and $R$ is a closed two-dimensional region. Divide the region $R$ into $n$ subregions $\Delta R_p$ of area $\Delta A_p$ and let $(x_p, y_p)$ be any point in subregion $\Delta R_p$. If the sum
\[S = \sum_{p=1}^n f(x_p, y_p) \Delta A_p\]tends to a unique limit $I$ as $n \to \infty$, then this is called the double integral of $f$ over the region $R$ and is denoted by
\[I = \int_R f(x, y) dA \cong \iint_R f(x, y) \,dx \,dy\]
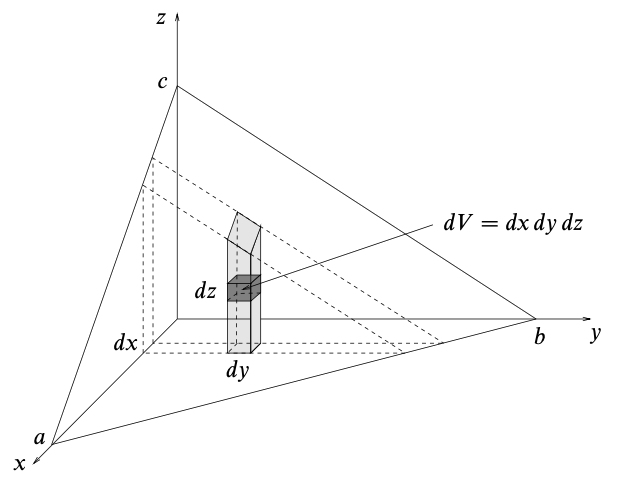
Definition. Suppose that $f(x, y, z)$ is a function and $R$ is a closed three-dimensional region. Divide the region $R$ into $n$ subregions $\Delta R_p$ of volume $\Delta V_p$ and let $(x_p, y_p, z_p)$ be any point in subregion $\Delta R_p$. If the sum
\[S = \sum_{p=1}^n f(x_p, y_p, z_p) \Delta V_p\]tends to a unique limit $I$ as $n \to \infty$, then this is called the triple integral of $f$ over the region $R$ and is denoted by
\[I = \int_R f(x, y) dV \cong \iiint_R f(x, y, z) \,dx \,dy \,dz\]
These ideas can be extended to define multiple integrals of higher dimensionality.
Change of Variables
Definition. The Jacobian of $(x, y)$ with respect to $(u, v)$ is the determinant of Jacobian matrix, i.e.
\[J(u, v) = { \partial (x, y) \over \partial (u, v) } = \begin{vmatrix} \dfrac{\partial x}{\partial u} & \dfrac{\partial x}{\partial v} \\ \dfrac{\partial y}{\partial u} & \dfrac{\partial y}{\partial v} \end{vmatrix}\]
Proposition. Consider a change of variables $(x, y) \to (u, v)$. Then
\[\iint_R dx\,dy \,f(x, y) = \iint_{R'} du\,dv \, \left|{ \partial (x, y) \over \partial (u, v) }\right| \,f(x(u, v), y(u, v))\]Proof.
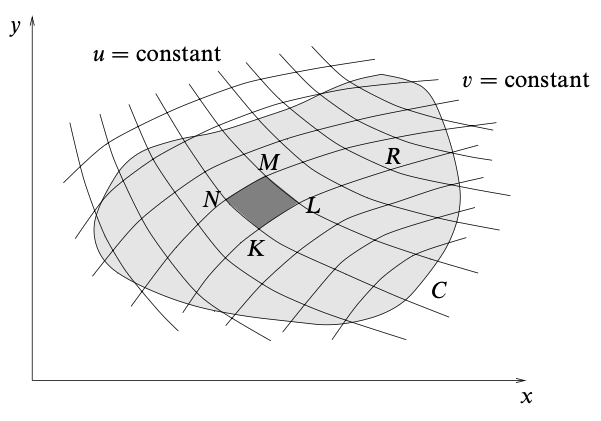
The new subregion $KLMN$ is approximately a parallelogram.
Since $v$ is constant along the line $KL$, we have
\[\vec{KL} = \left({\partial x \over \partial u} du \right)\mathbf{i} + \left({\partial y \over \partial u} du \right) \mathbf{j}\]Similarily, since $u$ is constant along the line $KN$, we have
\[\vec{KN} = \left({\partial x \over \partial v} dv \right)\mathbf{i} + \left({\partial y \over \partial v} dv \right) \mathbf{j}\]Thus, the area of the subregion is given by
\[\begin{align*} dA_{uv} = |\vec{KL} \times \vec{KN}| &= \left| {\partial x \over \partial u} du {\partial y \over \partial v} dv - {\partial x \over \partial v} dv {\partial y \over \partial u} du \right| \\ &= \left| {\partial x \over \partial u} {\partial y \over \partial v} - {\partial x \over \partial v} {\partial y \over \partial u} \right| \,du\,dv \\ &= \left| { \partial (x, y) \over \partial (u, v) } \right| \,du\,dv \end{align*}\]Therefore, when transforming the coordinates from $x, y$ to $u, v$, we can substitute $dx\,dy$ by the above, together with a different integrand and limits.
Example. [Gaussian Integral] Let
\[I = \int_{-\infty}^{\infty} e^{-x^2} \,dx\]We have
\[\begin{align*} I^2 &= \left( \int_{-\infty}^{\infty} e^{-x^2} \,dx \right) \left( \int_{-\infty}^{\infty} e^{-y^2} \,dx \right) \\ &= \int_{-\infty}^{\infty} dx \int_{-\infty}^{\infty} dy \, e^{-(x^2 + y^2)} \\ &= \iint_R e^{-(x^2 + y^2)} \,dx\,dy \end{align*}\]where the region $R$ is the whole $xy$-plane. By transforming to polar coordinates,
\[I^2 = \iint_{R'} e^{-r^2} r \,dr \,d\theta = \int_0^{2\pi} d\theta \int_0^{\infty} dr \,re^{-r^2} = 2\pi \Bigl[ -{1 \over 2}e^{-r^2}\Bigr]_0^{\infty} = \pi\]More rigorously, consider the integral
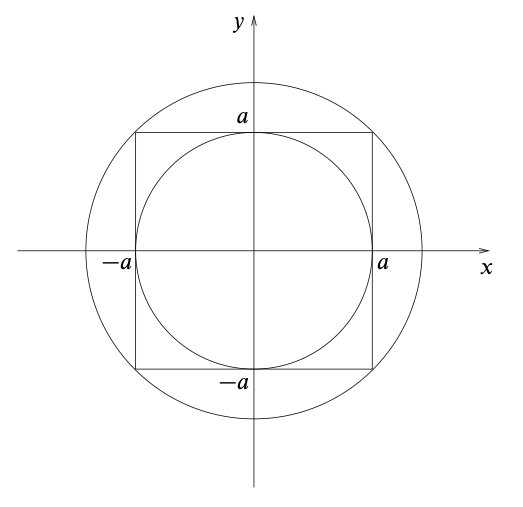
\[I(a) = \int_{-a}^a e^{-x^2} \,dx\]and similarily, we have
\[I^2(a) = \iint_R e^{-(x^2 + y^2)} \,dx\,dy\]where the region $R$ is the square of side $2a$ centred on the origin. The value of integral is therefore bounded by inner circle with radius $a$ and outer circle with radius $\sqrt{2}a$.
By transforming to polar coordinates, we have
\[\pi \left( 1 - e^{-a^2} \right) < I^2(a) < \pi \left( 1 - e^{-2a^2} \right)\]and hence $I^2(a) \to \pi$ as $a \to \infty$ so
\[\int_{-\infty}^{\infty} e^{-x^2} \,dx = \sqrt{\pi}\]
Definition. The Jacobian of $(x, y, z)$ with respect to $(u, v, w)$ is the determinant of the Jacobian matrix, i.e.
\[J(u, v, w) = { \partial (x, y, z) \over \partial (u, v, w) } = \begin{vmatrix} \dfrac{\partial x}{\partial u} & \dfrac{\partial x}{\partial v} & \dfrac{\partial x}{\partial w} \\ \dfrac{\partial y}{\partial u} & \dfrac{\partial y}{\partial v} & \dfrac{\partial y}{\partial w} \\ \dfrac{\partial z}{\partial u} & \dfrac{\partial z}{\partial v} & \dfrac{\partial z}{\partial w} \\ \end{vmatrix}\]
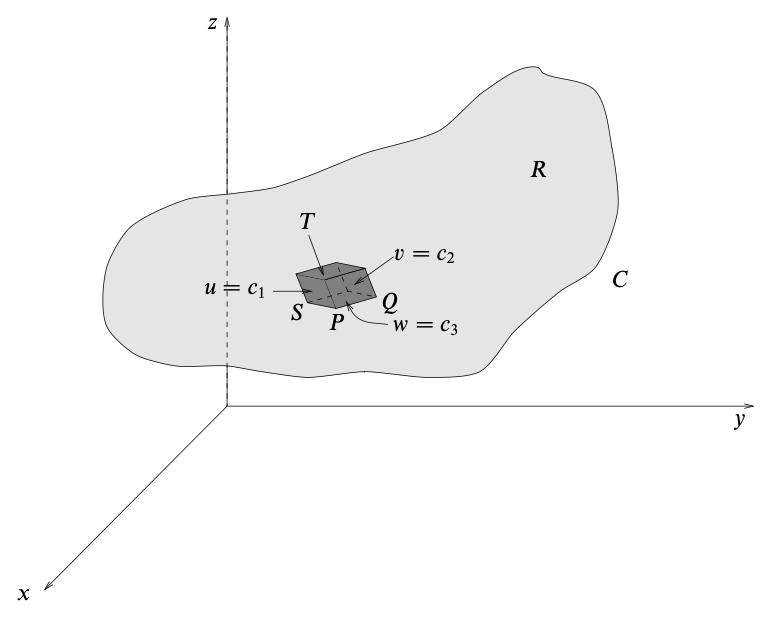
Proposition. Consider a change of variables $(x, y, z) \to (u, v, w)$. Then
\[\iiint_R dx\,dy\,dz \,f(x, y, z) = \iiint_{R'} du\,dv\,dw \, \left|{ \partial (x, y, z) \over \partial (u, v, w) }\right| \,f(x(u, v, w), y(u, v, w), z(u, v, w))\]Proof.
Similar to the argument presented in double integral, the new subregion is approximately a parallelepiped. The volume of that is given by the scalar triple product, i.e.
\[dV_{uvw} = \left| { \partial (x, y, z) \over \partial (u, v, w) } \right| \,du\,dv\,dw\]
References
- David Tong Vector Calculus Lecture Notes, 2024 - Chapter 2.1
- K.F. Riley Mathematical Methods for Physicists and Engineers, 1998 - Chapter 6