Complex Numbers

Definition. A complex number is a number $z \in \mathbb{C}$ of the form $z = a + bi$ where $a, b \in \mathbb{R}$ and $i^2 = -1$. We called $a = \text{Re}(z)$ the real part and $b = \text{Im}(z)$ the imaginary part.

Theorem. The representation of a complex number $z$ in terms of its real and imaginary parts is unique.

Proof.

Let $a, b, c, d \in \mathbb{R}$ such that

\[\begin{align*} a + bi &= c + di \\ (a-c)^2 &= -(d-b)^2 \end{align*}\]

As both $(a - c)^2 \ge 0$ and $(d - b)^2 \ge 0$, the equation is only possible with $a - c = 0$ and $b - d = 0$.

Hence, the representation is unique and if $z_1 = z_2$, then $\text{Re}(z_1) = \text{Re}(z_2)$ and $\text{Im}(z_1) = \text{Im}(z_2)$.

Definition. Let $z_1 = a + bi$ and $z_2 = c + di$, in order to follow the arithmetic rules for reals, together with the rule $i^2 = 1$, we have

  • Addition/Subtraction

    \[z_1 \pm z_2 = (a + c) \pm (b + d)i\]

  • Multiplication

    \[z_1z_2 = (ac - bd) + (ad + bc)i\]

  • Inverse

    \[z^{-1} = {1 \over z} = {a \over a^2 + b^2} + {-b \over a^2 + b^2}i\]

  • Division

    \[z_1/z_2 = z_1z_2^{-1}\]

Complex Conjugate

Definition. The complex conjugate $z^\ast$ (or $\bar{z}$) of $z = a + bi$ is $z^{\ast} = a - bi$.

Proposition. $(z^\ast)^\ast = z$.

Proposition. $z = z^\ast$ iff $z \in \mathbb{R}$. $z = -z^\ast$ iff $z$ is pure imaginary.

Proposition. If $zw \in \mathbb{R}$, then $z = \lambda w^\ast$ for some $\lambda \in \mathbb{R}$.

Proof.

As $zw = (zw)^\ast$,

\[{z \over w^\ast} = {z^\ast \over w} = \left({z \over w^\ast}\right)^\ast\]

Hence, $z / w^\ast = \lambda \in \mathbb{R}$ and $z = \lambda w^\ast$.

Proposition. Conjugation is distributive over addition, subtraction, multiplication and inverse, i.e.

  • $(z_1 \pm z_2)^\ast = z_1^\ast \pm z_2^\ast$

  • $(z_1z_2)^\ast = z_1^\ast z_2^\ast$

  • $(z^{-1})^\ast = (z^\ast)^{-1}$

Hence, we also have $(z^n)^\ast = (z^\ast)^n$.

The complex conjugate can be useful for converting complex fraction to a complex number:

\[{z_1 \over z_2} = \left({z_1 \over z_2}\right) \left({z_2^\ast \over z_2^\ast}\right) = {ac + bd \over c^2 + d^2} + {bc - ad \over c^2 + d^2}i\]

Definition. Given a complex-valued function $f$, the complex conjugate function $f^\ast$ is defined by

\[f^\ast(z^\ast) = [f(z)]^\ast \implies f^\ast(z) = [f(z^\ast)]^\ast\]

For example, let $f(z) = pz^2 + qz + r$, we have

\[f^\ast(z^\ast) = (pz^2 + qz + r)^\ast = p^\ast(z^\ast)^2 + q^\ast z^\ast + r^\ast \implies f^\ast(z) = p^\ast z^2 + q^\ast z + r^\ast\]

Modulus

Definition. The modulus $\vert z \vert$ of $z$ is defined by

\[|z| = \sqrt{a^2 + b^2}\]

Lemma. $\vert z^\ast \vert = \vert z \vert$.

Lemma. $zz^\ast = \vert z \vert^2$.

Lemma. $z^{-1} = z^\ast / \vert z \vert^2$.

Theorem. $\vert z_1z_2 \vert = \vert z_1 \vert \vert z_2 \vert$.

Proof.

\[\begin{align*} \vert (a + bi)(c + di) \vert^2 &= \vert (ac - bd) + (ad + bc)i \vert^2 \\ &= (ac - bd)^2 + (ad + bc)^2 \\ &= (ac)^2 + (bd)^2 - 2abcd + (ad)^2 + (bc)^2 + 2abcd \\ &= a^2(c^2 + d^2) + b^2(c^2 + d^2) \\ &= (a^2 + b^2) + (c^2 + d^2) \\ &= \vert a + bi \vert^2 \vert c + di \vert^2 \end{align*}\]

Argument

Definition. The argument $\arg(z)$ of $z$ is defined by

\[\arg(z) = \tan^{-1}\left({b \over a}\right)\]

which has a period of $2\pi$.

Theorem. For any $z_1, z_2 \in \mathbb{C}$, with a period of $2\pi$,

  • $\arg(z_1z_2) = \arg(z_1) + \arg(z_2)$

  • $\arg(z^{-1}) = \arg(z^\ast) = - \arg(z)$

Proof.

Let $z_1 = a + bi$ and $z_2 = c + di$, we have

\[\begin{align*} \tan(\arg(z_1) + \arg(z_2)) &= {\tan \arg(z_1) + \tan \arg(z_2) \over 1 - \tan \arg(z_1) \tan \arg(z_2)} \\ &= {b/a + d/c \over 1 - bd / ac} \\ &= {ad + bc \over ac - bd} \\ &= \tan \arg(z_1z_2) \end{align*}\]

Hence, $\arg(z_1z_2) = \arg(z_1) + \arg(z_2)$.

By definition, $\arg(z_1^\ast) = \arg(z_1^{-1}) = -b/a = - \arg(z_1)$ as $\tan^{-1} x = - \tan^{-1} x$.

Argand Diagram

Definition. An Argand diagram is a diagram in which a complex number $z = x + yi$ is represented by a vector $\mathbf{p} = \begin{pmatrix} x \\ y \end{pmatrix}$ on Cartesian plane. The $xy$ plane is referred as complex plane with real axis and imaginary axis.

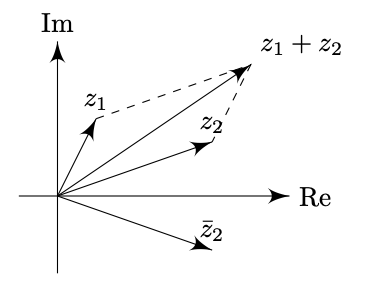
Argand Diagram

The Argand diagram allows us to interpret complex numbers geometrically, i.e.

Inequalities

By geometry, we observed the following inequalities about modulus:

Lemma. $\vert \text{Re}(z) \vert \le \vert z \vert$ and $\vert \text{Im}(z) \vert \le \vert z \vert$.

Theorem. [Triangle Inequality] If $z_1, z_2 \in \mathbb{C}$, then

\[\vert z_1 + z_2 \vert \le \vert z_1 \vert + \vert z_2 \vert\]

Proof.

Self-evident by geometry or algebraically

\[\begin{align*} 1 &= \text{Re} \left( {z_1 + z_2 \over z_1 + z_2} \right) \\ &= \text{Re} \left( {z_1 \over z_1 + z_2} \right) + \text{Re} \left( {z_2 \over z_1 + z_2} \right) \\ &\le \left\vert {z_1 \over z_1 + z_2} \right\vert + \left\vert {z_2 \over z_1 + z_2} \right\vert \end{align*}\]

Corollary. $\vert z_1 + z_2 + … + z_n \vert \le \vert z_1 \vert + \vert z_2 \vert + … + \vert z_n \vert$.

Lemma. $\vert z_1 - z_2 \vert$ is the distance between the two points represented by $z_1, z_2 \in \mathbb{C}$.

Proof.

By Pythagoras’ theorem.

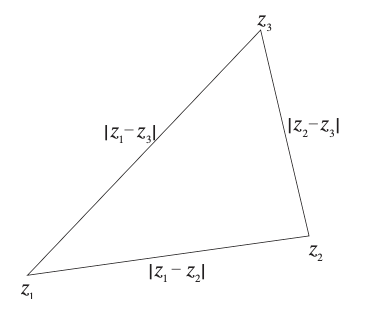
Triangle Inequality

Corollary. $|z_1 - z_3| \le |z_1 - z_2| + |z_2 + z_3|$.

Proof.

Self-evident by geometry or by substituting $z_1’ = z_1 - z_2$ and $z_2’ = z_2 - z_3$ into the triangle inequality.

Triangle Inequality

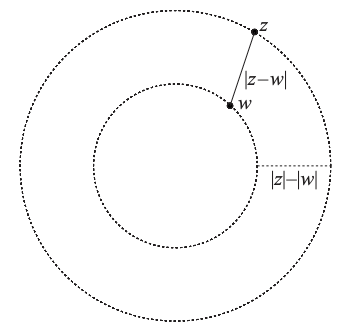
Corollary. $\vert z_1 - z_2 \vert \ge \vert \vert z_1 \vert - \vert z_2 \vert \vert$.

Proof.

Let $z_1 = z_1’ + z_2’$ and $z_2 = z_2’$, so $z_1’ = z_1 - z_2$ and $z_2’ = z_2$. Thus, we have

\[\vert z_1 \vert \le \vert z_1 - z_2 \vert + \vert z_2 \vert\]

which implies

\[\vert z_1 - z_2 \vert \ge \vert z_1 \vert - \vert z_2 \vert\]

Interchanging $z_1$ and $z_2$ we also have

\[\vert z_2 - z_1 \vert = \vert z_1 - z_2 \vert \ge \vert z_2 \vert - \vert z_1 \vert\]

Hence, combining both cases, we have $\vert z_1 - z_2 \vert \ge \vert \vert z_1 \vert - \vert z_2 \vert \vert$.

Corollary. $\vert z_1 + z_2 \vert \ge \vert \vert z_1 \vert - \vert z_2 \vert \vert$, which gives a lower bound of $\vert z_1 + z_2 \vert$.

Proof.

\[\vert z_1 \vert = \vert (z_1 + z_2) - z_2 \vert \le \vert z_1 + z_2 \vert + \vert -z_2 \vert = \vert z_1 + z_2 \vert + \vert z_2 \vert\]

which implies

\[\vert z_1 + z_2 \vert \ge \vert z_1 \vert - \vert z_2 \vert\]

Interchanging $z_1$ and $z_2$ we also have

\[\vert z_2 + z_1 \vert = \vert z_1 + z_2 \vert \ge \vert z_2 \vert - \vert z_1 \vert\]

Hence, combining both cases, we have $\vert z_1 + z_2 \vert \ge \vert \vert z_1 \vert - \vert z_2 \vert \vert$.

Polar Representation

The use of polar coordinates to represent position in Argand diagram is really helpful to understand some of the properties.

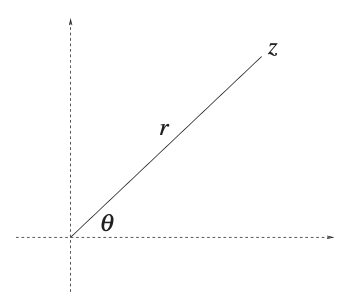
Polar Form

Definition. Let $x = r\cos\theta$ and $y = r\sin\theta$, the modolus/argument form of a complex number $z$ is

\[z = r(\cos\theta + i\sin\theta)\]

where $r = \vert z \vert$ is the modulus and $\theta = \arg(z)$ is the argument.

The pair $(r, \theta)$ specifies $z$ uniquely, but $z$ does not specify $(r, \theta)$ uniquely since $\arg(z)$ has a period of $2\pi$. Hence, we need to define the principal value of $\theta$ such that $-\pi < \theta \le \pi$.

Theorem. The principal value of $\theta \in (-\pi, \pi]$ is given by

\[\theta = 2\tan^{-1} \left( {y \over x + |z|} \right)\]

Proof.

$\tan^{-1}$ is single valued on the interval $(-{\pi \over 2}, {\pi \over 2})$. By the half-angle identity,

\[\tan {\theta \over 2} = {\sin \theta \over 1 + \cos \theta} = {y/r \over 1 + x/r} = {y \over x + r}\]

Hence, when $\theta \in (-\pi, \pi]$,

\[\theta = 2\tan^{-1} \left( {y \over x + |z|} \right)\]

The modulus/argument form is helpful to understand the geometric meaning of multiplication.

Theorem. Multiplication of $z_1$ by $z_2$ scales $z_1$ by $\vert z_2 \vert$ and rotates $z_1$ by $\arg(z_2)$.

Proof.

Let $z_1 = r_1(\cos \theta_1 + i \sin \theta_1)$ and $z_2 = r_2(\cos \theta_2 + i \sin \theta_2)$, then

\[\begin{align*} z_1z_2 &= r_1r_2((\cos \theta_1 \cos \theta_2 - \sin \theta_1 \sin \theta_2) + i (\sin \theta_1 \cos \theta_2 + \sin \theta_2 \cos \theta_1)) \\ &= r_1r_2(\cos (\theta_1 + \theta_2) + i \sin (\theta_1 + \theta_2)) \end{align*}\]

Hence, we have $\vert z_1z_2 \vert = \vert z_1 \vert \vert z_2 \vert$ and $\arg(z_1z_2) = \arg(z_1) + \arg(z_2)$ like we proved algebraically before.

Exponential Form

Consider the Taylor’s expansion of $\exp(x)$, $\sin(x)$ and $\cos(x)$, we have

\[e^{i\theta} = \cos \theta + i \sin \theta\]

Theorem. For any $z \in \mathbb{C}$, we have

\[z = r(\cos\theta + i\sin\theta) = re^{i\theta}\]

The geometric meaning of multiplication can easily be derived from the exponential form:

\[z_1z_2 = (r_1e^{i\theta_1})(r_2e^{i\theta_2}) = r_1r_2e^{i(\theta_1 + \theta_2)}\]

Corollary. $z^\ast = r(\cos\theta - i\sin\theta) = re^{-i\theta}$.

Corollary. For $w \in \mathbb{C}$,

\[\cos w = {1 \over 2} \left( e^{iw} + e^{-iw}\right) \quad\quad \sin w = {1 \over 2i} \left( e^{iw} - e^{-iw}\right)\]

Roots of Unity

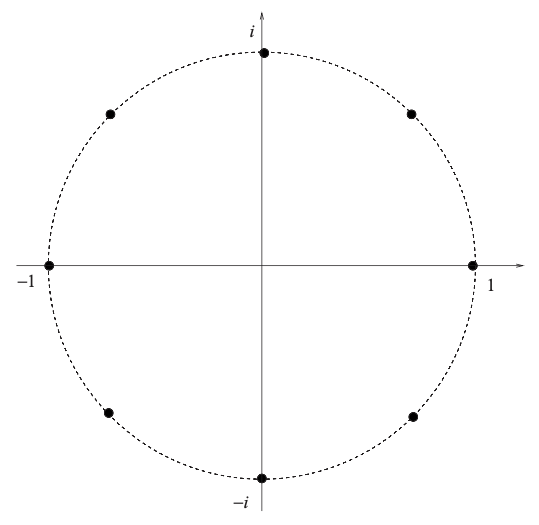
Theorem. Let $n$ be a positive integer. The n-th roots of unity are the distinct complex numbers

\[1, \omega, \omega^2, ..., \omega^{n-1}\]

where $\omega = e^{2\pi i/n}$, which are the $n$ distinct solutions of $z^n = 1$.

Proof.

Firstly, we have $\omega^n = e^{2\pi i} = 1$.

Let $k \in \set{0, 1, 2, …, n-1}$,

\[(\omega^k)^n = (\omega^n)^k = 1\]

Therefore, $1, \omega, \omega^2, …, \omega^{n-1}$ are solutions of $z^n = 1$. They are obviously distinct because $\arg(\omega^k) = 2\pi k/n$.

Conversely, suppose $z = re^{i\theta}$ is a solution of $z^n = 1$, we have $z^n = r^ne^{in\theta} = 1$. Therefore, $r^n = 1$ and $n\theta = 2k\pi$ with $k \in \mathbb{Z}$. Hence, we have $r = 1$ and by limiting $0 \le \theta < 2\pi$, $\theta = 2k\pi/n$ with $k = 0, 1, 2, …, n-1$.

The result can be generalized to equation $z^n = w$ with $w \not= 0$. Let $w = re^{i\theta}$ and $z_0 = r^{1/n}e^{i\theta/n}$, then $z_0^n = w$. Therefore, $(z/z_0)^n = 1$. Hence, $z_0, z_0\omega, z_0\omega^2, …, z_0\omega^{n-1}$ are the $n$ distinct solutions.

Furthermore, following from the sum of geometric series and $\omega^n = 1$,

\[1 + \omega + \omega^2 + ... + \omega^{n-1} = {1 - \omega^n \over 1 - \omega} = 0\]

Geometrically, the n-th roots of unity are the vertices of a regular n-gon on the complex plane, which are evenly spaced around a circle.

Roots of Unity

Logarithms and Powers

Definition. For $z \in \mathbb{C}$, $\log(z)$ is defined as “the” solution $w$ of $e^w = z$. Hence, by definition, we have

\[\exp(\log(z)) = z\]

and given $w = \log(z)$,

\[\begin{align*} \log(\exp(w)) &= \log(\exp(\log(z))) \\ &= \log(z) \\ &= w \end{align*}\]

Theorem. $\log(z) = \log(|z|) + i\arg(z)$.

Proof.

Let $z = re^{i\theta}$ and $w = \log(z) = x + yi$. From the definition, we have

\[z = \exp(w) = e^{x + yi} = (e^x)(e^{iy}) = re^{i\theta}\]

Hence,

\[\begin{align*} x &= \log(r) = \log(|z|) \\ y &= \theta + 2k\pi = \arg(z) \end{align*}\]

which is multi-valued as $\arg(z)$ is multi-valued function.

Definition. The principal value of $\log(z)$ is $-\pi < \arg(z) = \text{Im}(\log(z)) \le \pi$.

Although $\log(-1)$ has no solution in real, under complex logarithms, we have

\[\log(-1) = \log(1) + i\pi\]

Corollary. Similar to real logarithm, $\log(z_1z_2) = \log(z_1) + \log(z_2)$

Proof.

\[\begin{align*} \log(z_1z_2) &= \log(\vert z_1 \vert \vert z_2 \vert) + i \arg(z_1z_2) \\ &= \log(\vert z_1 \vert) + i\arg(z_1) + \log(\vert z_2 \vert) + i \arg(z_2) \\ &= \log(z_1) + \log(z_2) \end{align*}\]

Base on the definition of complex logarithm, we can now define the complex power of a complex number.

Definition. For $z \not = 0$ and $z, w \in \mathbb{C}$, $z$ to the complex power of $w$ is

\[z^w = e^{w \log z}\]

Since $\log(z)$ is multi-valued, $z^w$ is only defined to an arbitrary multiple of $e^{2k\pi i w}$.

De Moivre’s Theorem

Theorem. [De Moivre’s Theorem] For $\theta \in \mathbb{R}$ and $n \in \mathbb{Z}$,

\[\cos n\theta + i\sin n\theta = (\cos \theta + i\sin \theta)^n\]

Proof.

As $\cos \theta + i\sin \theta = e^{i\theta}$, we have

\[\begin{align*} \cos n\theta + i \sin n\theta &= e^{i(n\theta)} \\ &= (e^{i\theta})^n \\ &= (\cos \theta + i \sin \theta)^n \end{align*}\]

The theorem can be extended to $\theta, n \in \mathbb{C}$ with $\cos n \theta + i \sin n \theta$ equals to one of the values of $(\cos \theta + i\sin \theta)^n$.

Complex Plane Geometry

Lines

Theorem. For $z_0, w \in \mathbb{C}$ with $w \not = 0$ and varying $\lambda \in \mathbb{R}$, the equation

\[z = z_0 + \lambda w\]

represents points on a straight line passing through $z_0$ and parallel to $w$, which is similar to point-slope form.

Corollary. An alternative representation of a line passing through $z_0$ and parallel to $w$ in complex plane is

\[zw^\ast -z^\ast w = z_0w^\ast - z_0^\ast w\]

Proof.

As $\lambda \in \mathbb{R}$, $\lambda = \lambda^\ast$, we have

\[{z - z_0 \over w} = {z^\ast - z_0^\ast \over w^\ast}\]

The equation can be derived from reordering of the terms.

Hence,

Theorem. The general representation of a line is

\[a^\ast z + az^\ast + b = 0\]

Let $u, v \in \mathbb{C}$ be two points, then

\[a = v -u \quad \text{and} \quad b = \|u\|^2 + \|v\|^2 \in \mathbb{R}\]

Proof.

Given $u, v \in \mathbb{C}$, the points that are equidistant from them, i.e.

\[|z - u|^2 = |z - v|^2\]

form a straight line.

As $|z - u|^2 = (z - u)(z^\ast - u^\ast)$ and $|z - v|^2 = (z - v)(z^\ast - v^\ast)$, we have

\[(v^\ast - u^\ast)z + (v - u)z^\ast + |u|^2 + |v|^2 = 0\]

Practically, it will be more useful to represent the straight line passing through two points $u$ and $v$ as parametric form

\[z - u = \lambda(v - u) \quad \text{or} \quad z = (1 - \lambda)u + \lambda v\]

Details about different forms can be found here and here.

Circles

Theorem. The points on a circle in the complex plane with centre $w$ and radius $r$ is given by the equation

\[|z - w| = r\]

Since $r^2 = |z - w|^2 = (z - w)(z^\ast - w^\ast)$, the general form of a circle is

\[zz^\ast - (zw^\ast + z^\ast w) + |w|^2 = r^2\]

References